2 The free theory: Lagrangian, gauge symmetries and BRST differential
The starting point is a free theory in  , whose Lagrangian action is
written as the sum between the Lagrangian action of an Abelian BF model with
a maximal field spectrum (a single scalar field
, whose Lagrangian action is
written as the sum between the Lagrangian action of an Abelian BF model with
a maximal field spectrum (a single scalar field  , two types of
one-forms
, two types of
one-forms  and
and  , two kinds of two-forms
, two kinds of two-forms
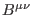 and
and
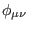 , and one three-form
, and one three-form
 ) and the
Lagrangian action of a free, massless tensor field with the mixed symmetry
) and the
Lagrangian action of a free, massless tensor field with the mixed symmetry 
 (meaning it is antisymmetric in its first two
indices
(meaning it is antisymmetric in its first two
indices
 and fulfills the
identity
and fulfills the
identity
![$ t_{[\mu \nu \vert\alpha ]}\equiv 0$](img18.png) )
)
where we used the notations
Everywhere in this paper the notations
![$ [\mu \nu \ldots \rho ]$](img29.png) and
and
 signify complete antisymmetry and respectively complete
symmetry with respect to the (Lorentz) indices between brackets, with the
conventions that the minimum number of terms is always used and the result
is never divided by the number of terms. It is convenient to work with the
Minkowski metric tensor of `mostly plus' signature
signify complete antisymmetry and respectively complete
symmetry with respect to the (Lorentz) indices between brackets, with the
conventions that the minimum number of terms is always used and the result
is never divided by the number of terms. It is convenient to work with the
Minkowski metric tensor of `mostly plus' signature
 and with the
five-dimensional Levi-Civita symbol
and with the
five-dimensional Levi-Civita symbol
 defined according to the convention
defined according to the convention
 .
.
Action (1) is found invariant under the gauge transformations
where all the gauge parameters are bosonic, with
 ,
,
 ,
,
 , and
, and
 completely antisymmetric and
completely antisymmetric and
 symmetric. By
symmetric. By  we denoted collectively all the gauge parameters as
we denoted collectively all the gauge parameters as
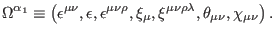 |
(10) |
The gauge transformations given by (4)-(7) are off-shell
reducible of order three (the reducibility relations hold everywhere in the
space of field history, and not only on the stationary surface of field
equations). This means that:
- there exist some transformations of the gauge parameters (8
)
 |
(11) |
such that the gauge transformations of all fields vanish strongly
(first-order reducibility relations)
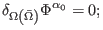 |
(12) |
- there exist some transformations of the first-order reducibility
parameters
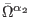
 |
(13) |
such that the gauge parameters vanish strongly (second-order reducibility
relations)
 |
(14) |
- there exist some transformations of the second-order reducibility
parameters
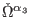
 |
(15) |
such that the first-order reducibility parameters vanish strongly
(third-order reducibility relations)
 |
(16) |
- there is no nontrivial transformation of the third-order reducibility
parameters
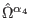 that annihilates all the
second-order reducibility parameters
that annihilates all the
second-order reducibility parameters
 |
(17) |
This is indeed the case for the model under study. In this
situation a complete set of first-order reducibility parameters
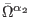 is given by
is given by
 |
(18) |
and transformations (9) have the form
with
 ,
,
 , and
, and
 completely antisymmetric.
Further, a complete set of second-order reducibility parameters
completely antisymmetric.
Further, a complete set of second-order reducibility parameters
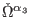 can be taken as
can be taken as
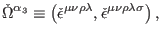 |
(22) |
and transformations (11) are
where both
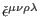 and
and
 are some arbitrary, bosonic, completely
antisymmetric tensors. Next, a complete set of third-order reducibility
parameters
are some arbitrary, bosonic, completely
antisymmetric tensors. Next, a complete set of third-order reducibility
parameters
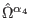 is represented by
is represented by
 |
(25) |
and transformations (13) can be chosen of the form
 |
(26) |
with
 an arbitrary,
completely antisymmetric tensor. Finally, it is easy to check (15
). Indeed, we work in
an arbitrary,
completely antisymmetric tensor. Finally, it is easy to check (15
). Indeed, we work in  , such that
, such that
 implies
implies
 .Since
.Since
 are arbitrary smooth functions that effectively depend on the spacetime
coordinates, it follows that the only possible choice is
are arbitrary smooth functions that effectively depend on the spacetime
coordinates, it follows that the only possible choice is
 .
.
We observe that the free theory under study is a usual linear gauge theory
(its field equations are linear in the fields), whose generating set of
gauge transformations is third-order reducible, such that we can define in a
consistent manner its Cauchy order, which is found to be equal to five.
In order to construct the BRST symmetry of this free theory, we introduce
the field/ghost and antifield spectra (2) and
The fermionic ghosts (25) correspond to the bosonic gauge parameters
(8), and therefore
 ,
,
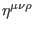 ,
,
 , and
, and
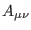 are completely
antisymmetric and
are completely
antisymmetric and
 is symmetric. The bosonic ghosts for ghosts
(26) are respectively associated with the first-order reducibility
parameters (16), such that
is symmetric. The bosonic ghosts for ghosts
(26) are respectively associated with the first-order reducibility
parameters (16), such that
 ,
,
 , and
, and
 are
completely antisymmetric. Along the same line, the fermionic ghosts for
ghosts for ghosts
are
completely antisymmetric. Along the same line, the fermionic ghosts for
ghosts for ghosts
 from (27) correspond to the
second-order reducibility parameters (20). As a consequence, the
ghost fields
from (27) correspond to the
second-order reducibility parameters (20). As a consequence, the
ghost fields
 and
and
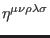 are again completely antisymmetric. Finally, the bosonic ghosts
for ghosts for ghosts for ghosts
are again completely antisymmetric. Finally, the bosonic ghosts
for ghosts for ghosts for ghosts
 from (27) are
associated with the third-order reducibility parameters (23), so
from (27) are
associated with the third-order reducibility parameters (23), so
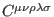 is also completely antisymmetric. The star
variables represent the antifields of the corresponding fields/ghosts. Their
Grassmann parities are obtained via the usual rule
is also completely antisymmetric. The star
variables represent the antifields of the corresponding fields/ghosts. Their
Grassmann parities are obtained via the usual rule
 , where we employed the notations
, where we employed the notations
 |
(34) |
It is understood that the antifields are endowed with the same
symmetry/antisymmetry properties like those of the corresponding
fields/ghosts.
Since both the gauge generators and the reducibility functions are
field-independent, it follows that the BRST differential reduces to
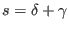 , where
, where 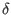 is the Koszul-Tate differential, and
is the Koszul-Tate differential, and  means the exterior longitudinal derivative. The Koszul-Tate
differential is graded in terms of the antighost number (
means the exterior longitudinal derivative. The Koszul-Tate
differential is graded in terms of the antighost number (
 ,
,
 ,
,
 ) and enforces a resolution of the algebra of smooth functions defined
on the stationary surface of field equations for action (1),
) and enforces a resolution of the algebra of smooth functions defined
on the stationary surface of field equations for action (1),
 ,
,
 . The exterior longitudinal derivative is
graded in terms of the pure ghost number (
. The exterior longitudinal derivative is
graded in terms of the pure ghost number (
 ,
,
 ,
,
 ) and is
correlated with the original gauge symmetry via its cohomology in pure ghost
number zero computed in
) and is
correlated with the original gauge symmetry via its cohomology in pure ghost
number zero computed in
 , which is
isomorphic to the algebra of physical observables for this free theory.
These two degrees of generators (2) and (25)-(31)
from the BRST complex are valued like
, which is
isomorphic to the algebra of physical observables for this free theory.
These two degrees of generators (2) and (25)-(31)
from the BRST complex are valued like
for
 . The actions of the differentials
. The actions of the differentials 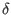 and
and  on the above generators read as
on the above generators read as
and respectively
The overall degree that grades the BRST complex is named ghost number (
 ) and is defined like the difference between the pure ghost
number and the antighost number, such that
) and is defined like the difference between the pure ghost
number and the antighost number, such that
 .
.
The BRST symmetry admits a canonical action
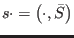 , where its canonical generator (
, where its canonical generator (
 ,
,
 ) satisfies the classical master
equation
) satisfies the classical master
equation
 . The symbol
. The symbol  denotes the
antibracket, defined by decreeing the fields/ghosts conjugated with the
corresponding antifields. In the case of the free theory under discussion
the solution to the master equation takes the form
denotes the
antibracket, defined by decreeing the fields/ghosts conjugated with the
corresponding antifields. In the case of the free theory under discussion
the solution to the master equation takes the form
The solution to the master equation encodes all the information on the gauge
structure of a given theory. We remark that in our case solution (53)
decomposes into terms with antighost numbers ranging from zero to four. Let
us briefly recall the significance of the various terms present in the
solution to the master equation. Thus, the part with the antighost number
equal to zero is nothing but the Lagrangian action of the gauge model under
study. The components of antighost number equal to one are always
proportional with the gauge generators. If the gauge algebra were
non-Abelian, then there would appear terms simultaneously linear in the
antighost number two antifields and quadratic in the pure ghost number one
ghosts. The absence of such terms in our case shows that the gauge
transformations are Abelian. The terms from (53) with higher
antighost numbers give us information on the reducibility functions. If the
reducibility relations held on-shell, then there would appear components
linear in the ghosts for ghosts (ghosts of pure ghost number strictly
greater than one) and quadratic in the various antifields. Such pieces are
not present in (53) since the reducibility relations (10), (
12), and (14) hold off-shell. Other possible components in
the solution to the master equation offer information on the higher-order
structure functions related to the tensor gauge structure of the theory.
There are no such terms in (53) as a consequence of the fact that all
higher-order structure functions vanish for the theory under study.
Ashkbiz Danehkar
2018-03-26
![]() , whose Lagrangian action is
written as the sum between the Lagrangian action of an Abelian BF model with
a maximal field spectrum (a single scalar field
, whose Lagrangian action is
written as the sum between the Lagrangian action of an Abelian BF model with
a maximal field spectrum (a single scalar field ![]() , two types of
one-forms
, two types of
one-forms ![]() and
and ![]() , two kinds of two-forms
, two kinds of two-forms
![]() and
and
![]() , and one three-form
, and one three-form
![]() ) and the
Lagrangian action of a free, massless tensor field with the mixed symmetry
) and the
Lagrangian action of a free, massless tensor field with the mixed symmetry ![]()
![]() (meaning it is antisymmetric in its first two
indices
(meaning it is antisymmetric in its first two
indices
![]() and fulfills the
identity
and fulfills the
identity
![]() )
)
![]() is given by
is given by
![]() , where
, where ![]() is the Koszul-Tate differential, and
is the Koszul-Tate differential, and ![]() means the exterior longitudinal derivative. The Koszul-Tate
differential is graded in terms of the antighost number (
means the exterior longitudinal derivative. The Koszul-Tate
differential is graded in terms of the antighost number (
![]() ,
,
![]() ,
,
![]() ) and enforces a resolution of the algebra of smooth functions defined
on the stationary surface of field equations for action (1),
) and enforces a resolution of the algebra of smooth functions defined
on the stationary surface of field equations for action (1),
![]() ,
,
![]() . The exterior longitudinal derivative is
graded in terms of the pure ghost number (
. The exterior longitudinal derivative is
graded in terms of the pure ghost number (
![]() ,
,
![]() ,
,
![]() ) and is
correlated with the original gauge symmetry via its cohomology in pure ghost
number zero computed in
) and is
correlated with the original gauge symmetry via its cohomology in pure ghost
number zero computed in
![]() , which is
isomorphic to the algebra of physical observables for this free theory.
These two degrees of generators (2) and (25)-(31)
from the BRST complex are valued like
, which is
isomorphic to the algebra of physical observables for this free theory.
These two degrees of generators (2) and (25)-(31)
from the BRST complex are valued like
![]() , where its canonical generator (
, where its canonical generator (
![]() ,
,
![]() ) satisfies the classical master
equation
) satisfies the classical master
equation
![]() . The symbol
. The symbol ![]() denotes the
antibracket, defined by decreeing the fields/ghosts conjugated with the
corresponding antifields. In the case of the free theory under discussion
the solution to the master equation takes the form
denotes the
antibracket, defined by decreeing the fields/ghosts conjugated with the
corresponding antifields. In the case of the free theory under discussion
the solution to the master equation takes the form