We consider a plasma consisting of three components, namely a cool
electron-fluid (at temperature
 ), an inertialess hot
electron component with a nonthermal (
), an inertialess hot
electron component with a nonthermal (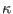 ) velocity
distribution, and uniformly distributed stationary ions.
) velocity
distribution, and uniformly distributed stationary ions.
The cool electron behavior is governed by the continuity equation,
 |
(2) |
and the momentum equation
 |
(3) |
The pressure of the cool electrons is governed by
 |
(4) |
Here 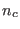 ,
,  and
and  are the number density, the velocity and the
pressure of the cool electron fluid,
are the number density, the velocity and the
pressure of the cool electron fluid, 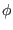 is the electrostatic wave
potential,
is the electrostatic wave
potential, 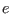 the elementary charge, and
the elementary charge, and
 denotes the
specific heat ratio (for
denotes the
specific heat ratio (for  degrees of freedom). We shall assume
degrees of freedom). We shall assume  (viz.,
(viz., 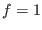 in 1D) for the adiabatic cool electrons.
in 1D) for the adiabatic cool electrons.
We assume the ions to be stationary (immobile), i.e., in a uniform state
 const. (where
const. (where  is the undisturbed ion density) at
all times. In order to obtain an expression for the number density of the hot
electrons,
is the undisturbed ion density) at
all times. In order to obtain an expression for the number density of the hot
electrons,  , based on the
, based on the 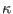 distribution (1), one may
integrate Eq. (1) over the velocity space, to obtain
[20]
distribution (1), one may
integrate Eq. (1) over the velocity space, to obtain
[20]
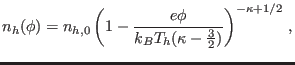 |
(5) |
where  and
and 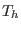 are the equilibrium number density and
“temperature” of the hot electrons, respectively, and
are the equilibrium number density and
“temperature” of the hot electrons, respectively, and 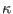 is the
spectral index measuring the deviation from thermal equilibrium.
is the
spectral index measuring the deviation from thermal equilibrium.
The densities of the (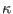 -distributed) hot electrons, the adiabatic cool
electrons, and the stationary ions are coupled via Poisson's equation:
-distributed) hot electrons, the adiabatic cool
electrons, and the stationary ions are coupled via Poisson's equation:
 |
(6) |
where
 is the permittivity constant,
is the permittivity constant,  and
and  are
the number density of hot electrons and ions, respectively.
are
the number density of hot electrons and ions, respectively.
At equilibrium, the plasma is quasi-neutral, so that
 |
(7) |
implying
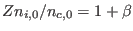 , where we have defined the hot-to-cool
electron density ratio
, where we have defined the hot-to-cool
electron density ratio
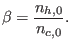 |
(8) |
According to Ref. [1], Landau damping is minimized in the
range
 , implying
, implying
 . This is our region of interest in what
follows, as nonlinear structures will not be sustainable for plasma
configurations for which the linear waves are strongly damped.
. This is our region of interest in what
follows, as nonlinear structures will not be sustainable for plasma
configurations for which the linear waves are strongly damped.
Scaling by appropriate quantities, we obtain the normalized set of equations
Here, 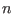 ,
,  and
and  denote the cool electron fluid density, velocity and
pressure variables normalized with respect to
denote the cool electron fluid density, velocity and
pressure variables normalized with respect to  ,
,
![$ c_{th}=\left[
k_{B}T_{h}/m_{e}\right] ^{1/2}$](img109.png) and
and
 , respectively. Time
and space were scaled by the plasma period
, respectively. Time
and space were scaled by the plasma period
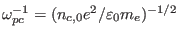 and the characteristic length
and the characteristic length
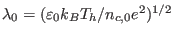 , respectively. Finally,
, respectively. Finally,
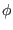 is the wave potential scaled by
is the wave potential scaled by
 . We have defined the
temperature ratio of the cool to the hot electrons as
. We have defined the
temperature ratio of the cool to the hot electrons as
 |
(13) |
Ashkbiz Danehkar
2018-03-28
![]() ), an inertialess hot
electron component with a nonthermal (
), an inertialess hot
electron component with a nonthermal (![]() ) velocity
distribution, and uniformly distributed stationary ions.
) velocity
distribution, and uniformly distributed stationary ions.
![]() const. (where
const. (where ![]() is the undisturbed ion density) at
all times. In order to obtain an expression for the number density of the hot
electrons,
is the undisturbed ion density) at
all times. In order to obtain an expression for the number density of the hot
electrons, ![]() , based on the
, based on the ![]() distribution (1), one may
integrate Eq. (1) over the velocity space, to obtain
[20]
distribution (1), one may
integrate Eq. (1) over the velocity space, to obtain
[20]
![]() -distributed) hot electrons, the adiabatic cool
electrons, and the stationary ions are coupled via Poisson's equation:
-distributed) hot electrons, the adiabatic cool
electrons, and the stationary ions are coupled via Poisson's equation: