2 Theoretical Model
We consider a 1-D collisionless, four-component
plasma consisting of cool inertial background electrons (at temperature
 ), mobile cool positrons (or electron holes; at temperature
), mobile cool positrons (or electron holes; at temperature
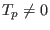 ),
inertialess hot suprathermal electrons modeled by a
),
inertialess hot suprathermal electrons modeled by a  -distribution (at
temperature
-distribution (at
temperature
 ), and uniformly distributed stationary ions.
), and uniformly distributed stationary ions.
The cool electrons and positrons are governed by the following fluid
equations:
where  ,
,  and
and  are the number density, the velocity and the pressure
of the cool electrons and positrons (denoted by indices `c' and
`p', respectively),
are the number density, the velocity and the pressure
of the cool electrons and positrons (denoted by indices `c' and
`p', respectively), 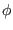 is the electrostatic wave potential,
is the electrostatic wave potential,  the elementary charge,
the elementary charge,  the electron mass,
the electron mass,  the positron mass,
and
the positron mass,
and
 denotes the specific heat ratio for
denotes the specific heat ratio for  degrees of
freedom. For the adiabatic cool electrons and positrons in one-dimensional (
degrees of
freedom. For the adiabatic cool electrons and positrons in one-dimensional ( ), we get
), we get
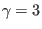 . Through this paper, we assume that
. Through this paper, we assume that
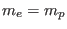 .
.
Following Eq. 1 in Ref. [31], the  -distribution
expression is obtained for the number density of the hot suprathermal
electrons:
-distribution
expression is obtained for the number density of the hot suprathermal
electrons:
![$\displaystyle n_{h}(\phi)=n_{h,0}\left[ 1-\frac{e\phi}{k_{B}T_{h}(\kappa-\tfrac{3}{2} )}\right] ^{-\kappa+1/2}\,,$](img78.png) |
(7) |
where 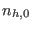 and
and 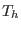 are the equilibrium number density and the
temperature of the hot electrons, respectively,
are the equilibrium number density and the
temperature of the hot electrons, respectively,  the Boltzmann
constant, and the spectral index
the Boltzmann
constant, and the spectral index  measures the deviation from thermal equilibrium.
For reality of the characteristic modified thermal velocity,
measures the deviation from thermal equilibrium.
For reality of the characteristic modified thermal velocity,
![$ \left[ (2\kappa-3)k_{B}T_{h}/\kappa m_{e}\right] ^{1/2}$](img81.png) , the spectral index must
take
, the spectral index must
take
 . The suprathermality is measured by the spectral index
. The suprathermality is measured by the spectral index  ,
describing how it deviates from a Maxwellian distribution, i.e., low values of
,
describing how it deviates from a Maxwellian distribution, i.e., low values of  are associated with a significant suprathermality; on the other hand, a
Maxwellian distribution is recovered in the limit
are associated with a significant suprathermality; on the other hand, a
Maxwellian distribution is recovered in the limit
 .
.
The ions are assumed to be immobile in a uniform state, i.e.,
 const. at all times, where
const. at all times, where 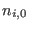 is the undisturbed ion density. The
plasma is quasi-neutral at equilibrium, so
is the undisturbed ion density. The
plasma is quasi-neutral at equilibrium, so
 ,
that implies
,
that implies
 |
(8) |
where we have defined the hot-to-cool electron density ratio as
 , and the positron-to-cool electron density ratio as
, and the positron-to-cool electron density ratio as
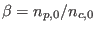 , while
, while 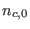 and
and  are the equilibrium
number densities of the cool electrons and positrons, respectively.
Electrostatic waves are weakly damped in the range of
are the equilibrium
number densities of the cool electrons and positrons, respectively.
Electrostatic waves are weakly damped in the range of
 [26,27,28,29], so
[26,27,28,29], so
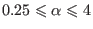 . This region may permit the propagation of nonlinear
electrostatic structures. As the positron fraction has been measured to be
. This region may permit the propagation of nonlinear
electrostatic structures. As the positron fraction has been measured to be
 in low energy solar wind observations [1,2,3,5] and
in low energy solar wind observations [1,2,3,5] and
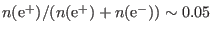 -0.1 in some laser-plasma experiences [14,15], we assume
-0.1 in some laser-plasma experiences [14,15], we assume
 .
.
All four components are coupled via the Poisson's equation:
 |
(9) |
where
 is the permittivity constant.
is the permittivity constant.
Scaling by appropriate quantities, we arrive at a fluid system of our model in
a dimensionless form for the cool electrons and the positrons, respectively:
The dimensionless Poisson's equation takes the following form:
where  and
and  denote the fluid density variables of the cool electrons
and positrons normalized with respect to
denote the fluid density variables of the cool electrons
and positrons normalized with respect to 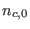 and
and  ,
respectively,
,
respectively,  and
and 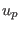 the velocity variables of the cool electrons and
positrons scaled by the hot electron thermal speed
the velocity variables of the cool electrons and
positrons scaled by the hot electron thermal speed
 ,
,  and
and  the pressure variables of the
cool electrons and positrons normalized with respect to
the pressure variables of the
cool electrons and positrons normalized with respect to
 and
and
 , respectively, and the wave potential
, respectively, and the wave potential 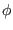 by
by
 , time and space scaled by the plasma period
, time and space scaled by the plasma period
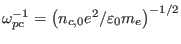 and the characteristic
length
and the characteristic
length
 , respectively. We have defined the cool-to-hot electron temperature
ratio as
, respectively. We have defined the cool-to-hot electron temperature
ratio as
 , and the positron-to-hot electron temperature
ratio as
, and the positron-to-hot electron temperature
ratio as
 . Landau damping is minimized if
. Landau damping is minimized if
 [26,27,28], and the same for the cool positrons, i.e.,
[26,27,28], and the same for the cool positrons, i.e.,
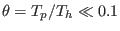 (see Ref. [40]), and typically
(see Ref. [40]), and typically
 in some laser-plasma experiences [14].
in some laser-plasma experiences [14].
Ashkbiz Danehkar
2018-03-28
![]() ), mobile cool positrons (or electron holes; at temperature
), mobile cool positrons (or electron holes; at temperature
![]() ),
inertialess hot suprathermal electrons modeled by a
),
inertialess hot suprathermal electrons modeled by a ![]() -distribution (at
temperature
-distribution (at
temperature
![]() ), and uniformly distributed stationary ions.
), and uniformly distributed stationary ions.
![]() -distribution
expression is obtained for the number density of the hot suprathermal
electrons:
-distribution
expression is obtained for the number density of the hot suprathermal
electrons:
![]() const. at all times, where
const. at all times, where ![]() is the undisturbed ion density. The
plasma is quasi-neutral at equilibrium, so
is the undisturbed ion density. The
plasma is quasi-neutral at equilibrium, so
![]() ,
that implies
,
that implies