Bibliography

1

D. Birmingham, M. Blau, M. Rakowski and G. Thompson, Topological field theory, Phys. Rept. 209 (1991) 129-340.

2

J. M. F. Labastida and C. Lozano, Lectures on topological quantum field theory, in Proceedings of La Plata-CERN-Santiago de Compostela Meeting on Trends in Theoretical Physics, La Plata, Argentina, April-May 1997, eds. H. Falomir, R. E. Gamboa Sarav í, F. A. Schaposnik (AIP, New York 1998), AIP Conference Proceedings vol. 419, 54-93 [arXiv:hep-th/9709192].

3

P. Schaller and T. Strobl, Poisson structure induced (topological) field theories, Mod. Phys. Lett. A9 (1994) 3129-3136 [arXiv:hep-th/9405110].

4

N. Ikeda, Two-dimensional gravity and nonlinear gauge theory, Annals Phys. 235 (1994) 435-464 [arXiv:hep-th/9312059].

5

A. Yu. Alekseev, P. Schaller and T. Strobl, Topological 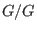$G/G$ WZW model in the generalized momentum representation, Phys. Rev. D52 (1995) 7146-7160 [arXiv:hep-th/9505012].

6

T. Klösch and T. Strobl, Classical and quantum gravity in 1+1 dimensions: I. A unifying approach, Class. Quantum Grav. 13 (1996) 965-983 [arXiv:gr-qc/9508020]; Erratum-ibid. 14 (1997) 825.

7

T. Klösch and T. Strobl, Classical and quantum gravity in 1+1 dimensions. II: The universal coverings, Class. Quantum Grav. 13 (1996) 2395-2421 [arXiv:gr-qc/9511081].

8

T. Klösch and T. Strobl, Classical and quantum gravity in 1+1 dimensions: III. Solutions of arbitrary topology, Class. Quantum Grav. 14 (1997) 1689-1723 [arXiv:hep-th/9607226].

9

A. S. Cattaneo and G. Felder, A path integral approach to the Kontsevich quantization formula, Commun. Math. Phys. 212 (2000) 591-611 [arXiv:math/9902090].

10

A. S. Cattaneo and G. Felder, Poisson sigma models and deformation quantization, Mod. Phys. Lett. A16 (2001) 179-189 [arXiv:hep-th/0102208].

11

C. Teitelboim, Gravitation and hamiltonian structure in two spacetime dimensions, Phys. Lett. B126 (1983) 41-45.

12

R. Jackiw, Lower dimensional gravity, Nucl. Phys. B252 (1985) 343-356.

13

M. O. Katanayev and I. V. Volovich, String model with dynamical geometry and torsion, Phys. Lett. B175 (1986) 413-416 [arXiv:hep-th/0209014].

14

J. Brown, Lower Dimensional Gravity, World Scientific, Singapore 1988.

15

M. O. Katanaev and I. V. Volovich, Two-dimensional gravity with dynamical torsion and strings, Annals Phys. 197 (1990) 1-32.

16

H.-J. Schmidt, Scale-invariant gravity in two dimensions, J. Math. Phys. 32 (1991) 1562-1566.

17

S. N. Solodukhin, Topological 2D Riemann-Cartan-Weyl gravity, Class. Quantum Grav. 10 (1993) 1011-1021.

18

N. Ikeda and K. I. Izawa, General form of dilaton gravity and nonlinear gauge theory, Prog. Theor. Phys. 90 (1993) 237-245 [arXiv:hep-th/9304012].

19

T. Strobl, Dirac quantization of gravity-Yang-Mills systems in 1+1 dimensions, Phys. Rev. D50 (1994) 7346-7350 [arXiv:hep-th/9403121].

20

D. Grumiller, W. Kummer and D. V. Vassilevich, Dilaton gravity in two dimensions, Phys. Rept. 369 (2002) 327-430 [arXiv:hep-th/0204253].

21

T. Strobl, Gravity in two space-time dimensions, Habilitation thesis RWTH Aachen, May 1999, arXiv:hep-th/0011240.

22

K. Ezawa, Ashtekar's formulation for N = 1, 2 supergravities as “constrained” BF theories, Prog. Theor. Phys. 95 (1996) 863-882 [arXiv:hep-th/9511047].

23

L. Freidel, K. Krasnov and R. Puzio, BF description of higher-dimensional gravity theories, Adv. Theor. Math. Phys. 3 (1999) 1289-1324 [arXiv:hep-th/9901069].

24

L. Smolin, Holographic formulation of quantum general relativity, Phys. Rev. D61 (2000) 084007 [arXiv:hep-th/9808191].

25

Y. Ling and L. Smolin, Holographic formulation of quantum supergravity, Phys. Rev. D63 (2001) 064010 [arXiv:hep-th/0009018].

26

K.-I. Izawa, On nonlinear gauge theory from a deformation theory perspective, Prog. Theor. Phys. 103 (2000) 225-228 [arXiv:hep-th/9910133].

27

C. Bizdadea, Note on two-dimensional nonlinear gauge theories, Mod. Phys. Lett. A15 (2000) 2047-2055 [arXiv:hep-th/0201059].

28

N. Ikeda, A deformation of three dimensional BF theory, J.High Energy Phys. JHEP11(2000)009 [arXiv:hep-th/0010096].

29

N. Ikeda, Deformation of BF theories, topological open membrane and a generalization of the star deformation, J. High Energy Phys. JHEP07(2001)037 [arXiv:hep-th/0105286].

30

C. Bizdadea, E. M. Cioroianu and S. O. Saliu, Hamiltonian cohomological derivation of four-dimensional nonlinear gauge theories, Int. J. Mod. Phys. A17 (2002) 2191-2210 [arXiv:hep-th/0206186].

31

C. Bizdadea, C. C. Ciobîrca, E. M. Cioroianu, S. O. Saliu and S. C. Sararu, Hamiltonian BRST deformation of a class of n-dimensional BF-type theories, J. High Energy Phys. JHEP01 (2003)049 [arXiv:hep-th/0302037].

32

E. M. Cioroianu and S. C. Sararu, Self-interactions in a topological BF-type model in D = 5, J. High Energy Phys. JHEP 07(2005)056 [arXiv:hep-th/0508035].

33

E. M. Cioroianu and S. C. Sararu, PT-symmetry breaking Hamiltonian interactions in BF models, Int. J. Mod. Phys. A21 (2006) 2573-2599 [arXiv:hep-th/0606164].

34

N. Ikeda, Chern-Simons gauge theory coupled with BF theory, Int. J. Mod. Phys. A18 (2003) 2689-2702 [arXiv:hep-th/0203043].

35

E. M. Cioroianu and S. C. Sararu, Two-dimensional interactions between a BF-type theory and a collection of vector fields, Int. J. Mod. Phys. A19 (2004) 4101-4125 [arXiv:hep-th/0501056].

36

C. Bizdadea, E. M. Cioroianu, S. O. Saliu and S. C. S araru, Couplings of a collection of BF models to matter theories, Eur. Phys. J. C41 (2005) 401-420 [arXiv:hep-th/0508037].

37

C. Bizdadea, E. M. Cioroianu, I. Negru, S. O. Saliu and S. C. Sararu, On the generalized Freedman-Townsend model, J. High Energy Phys. JHEP10(2006)004 [arXiv:0704.3407(hep-th)].

38

C. Bizdadea, E. M. Cioroianu, S. O. Saliu, S. C. Sa raru and M. Iordache, Four-dimensional couplings among BF and massless Rarita-Schwinger theories: a BRST cohomological approach, Eur. Phys. J. C58 (2008) 123-149 [arXiv:0812.3810(hep-th)].

39

G. Barnich and M. Henneaux, Consistent couplings between fields with a gauge freedom and deformations of the master equation, Phys. Lett. B311 (1993) 123-129 [arXiv:hep-th/9304057].

40

M. Henneaux, Consistent interactions between gauge fields: the cohomological approach, Contemp. Math. 219 (1998) 93 [arXiv:hep-th/9712226].

41

C. Bizdadea, Consistent interactions in the Hamiltonian BRST formalism, Acta Phys. Polon. B32 (2001) 2843-2862 [arXiv:hep-th/0003199].

42

G. Barnich, F. Brandt and M. Henneaux, Local BRST cohomology in the antifield formalism: I. General theorems, Commun. Math. Phys. 174 (1995) 57-91 [arXiv:hep-th/9405109].

43

G. Barnich, F. Brandt and M. Henneaux, Local BRST cohomology in the antifield formalism: II. Application to Yang-Mills theory, Commun. Math. Phys. 174 (1995) 93-116 [arXiv:hep-th/9405194].

44

G. Barnich, F. Brandt and M. Henneaux, Local BRST cohomology in gauge theories, Phys. Rept. 338 (2000) 439-569 [arXiv:hep-th/0002245].

45

N. Ikeda, Topological field theories and geometry of Batalin-Vilkovisky algebras, J. High Energy Phys. JHEP10 (2002)076 [arXiv:hep-th/0209042].

46

N. Ikeda and K.-I. Izawa, Dimensional reduction of nonlinear gauge theories, J. High Energy Phys. JHEP 09(2004)030 [arXiv:hep-th/0407243].

47

T. Curtright and P. G. O. Freund, Massive dual fields, Nucl. Phys. B172 (1980) 413-424.

48

T. Curtright, Generalized gauge fields, Phys. Lett. B165 (1985) 304-308.

49

C. S. Aulakh, I. G. Koh and S. Ouvry, Higher spin fields with mixed symmetry, Phys. Lett. B173 (1986) 284-288.

50

J. M. Labastida and T. R. Morris, Massless mixed-symmetry bosonic free fields, Phys. Lett. B180 (1986) 101-106.

51

J. M. Labastida, Massless particles in arbitrary representations of the Lorentz group, Nucl. Phys. B322 (1989) 185-209.

52

C. Burdik, A. Pashnev and M. Tsulaia, On the mixed symmetry irreducible representations of the Poincaré group in the BRST approach, Mod. Phys. Lett. A16 (2001) 731-746 [arXiv:hep-th/0101201].

53

Yu. M. Zinoviev, On massive mixed symmetry tensor fields in Minkowski space and $(A)dS$ [arXiv:hep-th/0211233].

54

C. M. Hull, Duality in gravity and higher spin gauge fields, J. High Energy Phys. JHEP09(2001)027 [arXiv:hep-th/0107149].

55

X. Bekaert and N. Boulanger, Massless spin-two field S-duality, Class. Quantum Grav. 20 (2003) S417-S423 [arXiv:hep-th/0212131].

56

X. Bekaert and N. Boulanger, On geometric equations and duality for free higher spins, Phys. Lett. B561 (2003) 183-190 [arXiv:hep-th/0301243].

57

H. Casini, R. Montemayor and L. F. Urrutia, Duality for symmetric second rank tensors. II. The linearized gravitational field, Phys. Rev. D68 (2003) 065011 [arXiv:hep-th/0304228].

58

N. Boulanger, S. Cnockaert and M. Henneaux, A note on spin-s duality, J. High Energy Phys. JHEP06(2003)060 [arXiv:hep-th/0306023].

59

P. de Medeiros and C. Hull, Exotic tensor gauge theory and duality, Commun. Math. Phys. 235 (2003) 255-273 [arXiv:hep-th/0208155].

60

X. Bekaert and N. Boulanger, Tensor gauge fields in arbitrary representations of 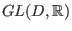$GL(D,\mathbb{R})$. Duality and Poincaré Lemma, Commun. Math. Phys. 245 (2004) 27-67 [arXiv:hep-th/0208058].

61

X. Bekaert and N. Boulanger, Tensor gauge fields in arbitrary representations of 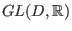$GL(D,\mathbb{R})$: II. Quadratic actions, Commun. Math. Phys. 271 (2007) 723-773 [arXiv:hep-th/0606198].

62

X. Bekaert, N. Boulanger and M. Henneaux, Consistent deformations of dual formulations of linearized gravity: A no-go result, Phys. Rev. D67 (2003) 044010 [arXiv:hep-th/0210278].

63

Yu. M. Zinoviev, First order formalism for mixed symmetry tensor fields [arXiv:hep-th/0304067].

64

Yu. M. Zinoviev, First order formalism for massive mixed symmetry tensor fields in Minkowski and $(A)dS$ spaces [arXiv:hep-th/0306292].

65

N. Boulanger and L. Gualtieri, An exotic theory of massless spin-2 fields in three dimensions, Class. Quantum Grav. 18 (2001) 1485-1502 [arXiv:hep-th/0012003].

66

S. C. Anco, Parity violating spin-two gauge theories, Phys. Rev. D67 (2003) 124007 [arXiv:gr-qc/0305026].

67

A. K. Bengtsson, I. Bengtsson and L. Brink, Cubic interaction terms for arbitrary spin, Nucl. Phys. B227 (1983) 31-40.

68

M. A. Vasiliev, Cubic interactions of bosonic higher spin gauge fields in $AdS_5$, Nucl. Phys. B616 (2001) 106-162 [arXiv:hep-th/0106200]; Erratum-ibid. B652 (2003) 407.

69

E. Sezgin and P. Sundell, $7D$ bosonic higher spin gauge theory: symmetry algebra and linearized constraints, Nucl. Phys. B634 (2002) 120-140 [arXiv:hep-th/0112100].

70

D. Francia and A. Sagnotti, Free geometric equations for higher spins, Phys. Lett. B543 (2002) 303-310 [arXiv:hep-th/0207002].

71

C. Bizdadea, C. C. Ciobîrca, E. M. Cioroianu, I. Negru, S. O. Saliu and S. C. Sararu, Interactions of a single massless tensor field with the mixed symmetry (3,1). No-go results, J. High Energy Phys. JHEP10(2003)019.

72

N. Boulanger and S. Cnockaert, Consistent deformations of [p,p]-type gauge field theories, J. High Energy Phys. JHEP 03(2004)031 [arXiv:hep-th/0402180].

73

C. C. Ciobîrca, E. M. Cioroianu and S. O. Saliu, Cohomological BRST aspects of the massless tensor field with the mixed symmetry (k,k), Int. J. Mod. Phys. A19 (2004) 4579-4619 [arXiv:hep-th/0403017].

74

C. Bizdadea, C. C. Ciobîrca, E. M. Cioroianu, S. O. Saliu and S. C. Sararu, Interactions of a massless tensor field with the mixed symmetry of the Riemann tensor. No-go results, Eur. Phys. J. C36 (2004) 253-270 [arXiv:hep-th/0306154].

75

X. Bekaert, N. Boulanger and S. Cnockaert, No self-interaction for two-column massless fields, J. Math. Phys. 46 (2005) 012303 [arXiv:hep-th/0407102].

76

N. Boulanger, S. Leclercq and S. Cnockaert, Parity-violating vertices for spin-3 gauge fields, Phys.Rev. D73 (2006) 065019 [arXiv:hep-th/0509118].

77

X. Bekaert, N. Boulanger and S. Cnockaert, Spin three gauge theory revisited, J. High Energy Phys. JHEP01(2006)052 [arXiv:hep-th/0508048].

78

C. Bizdadea, C. C. Ciobîrca, I. Negru and S. O. Saliu, Couplings between a single massless tensor field with the mixed symmetry (3,1) and one vector field, Phys.Rev. D74 (2006) 045031 [arXiv:0705.1048(hep-th)].

79

C. Bizdadea, C. C. Ciobîrca, E. M. Cioroianu and S. O. Saliu, Interactions between a massless tensor field with the mixed symmetry of the Riemann tensor and a massless vector field, J. Phys. A: Math. Gen. 39 (2006) 10549-10564 [arXiv:0705.1054(hep-th)].

80

C. Bizdadea, D. Cornea and S. O. Saliu, No cross-interactions among different tensor fields with the mixed symmetry (3, 1) intermediated by a vector field, J. Phys. A: Math. Theor. 41 (2008) 285202 [arXiv:0901.4059(hep-th)].