F. Deformed gauge structure
If we denote by
 and
and
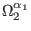 two independent sets of gauge parameters,
two independent sets of gauge parameters,
then the concrete form of the commutators among the deformed gauge
transformations of the fields associated with (285) and (286) (and
generically written as in (162)) read as
![$\displaystyle \left[ \bar{\delta}_{\Omega _{1}},\bar{\delta}_{\Omega _{2}}\right] \varphi =0,$](img834.png) |
(401) |
![$\displaystyle \left[ \bar{\delta}_{\Omega _{1}},\bar{\delta}_{\Omega _{2}}\right] V_{\mu }= \bar{\delta}_{\Omega }V_{\mu },$](img838.png) |
(404) |
 |
(405) |
![$\displaystyle \left[ \bar{\delta}_{\Omega _{1}},\bar{\delta}_{\Omega _{2}}\righ...
...\frac{\delta S^{\mathrm{L} }}{\delta H^{[\mu }}\frac{d\xi _{\nu ]}}{d\varphi },$](img840.png) |
(406) |
 |
(407) |
![$\displaystyle \left[ \bar{\delta}_{\Omega _{1}},\bar{\delta}_{\Omega _{2}}\right] t_{\mu \nu \vert\alpha }=0.$](img842.png) |
(408) |
The gauge parameters from the right-hand side of the above formulas are
defined through
 |
(409) |
where
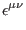 |
 |
 |
(410) |
| |
|
 |
(411) |
| |
|
![$\displaystyle \left. +\tfrac{1}{2}K^{\mu \nu \rho }\left( \epsilon ^{(1)}\xi _{...
...da }-\xi _{\lambda }^{(2)}\xi
^{(1)\mu \nu \rho \lambda }\right) \right] \notag$](img847.png) |
(412) |
| |
|
 |
(413) |
| |
|
 |
(414) |
| |
|
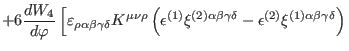 |
(415) |
| |
|
![$\displaystyle \left. +\tfrac{1}{6}\varepsilon ^{\mu \nu \rho \lambda \sigma }\v...
...pha ^{\prime }\beta ^{\prime }\gamma
^{\prime }\delta ^{\prime }}\right] \notag$](img851.png) |
(416) |
| |
|
![$\displaystyle \left. -\tfrac{1}{2}\varepsilon ^{\mu \nu \rho \lambda \sigma }\f...
...}\right) -2V_{\rho }\xi _{\lambda
}^{(1)}\xi _{\sigma }^{(2)}\right] \right\} ,$](img852.png) |
(417) |
In addition, we made the notations
 |
(425) |
Related to the first-order reducibility, the transformations (163)
are given by
 |
(430) |
 |
(434) |
 |
(435) |
 |
(436) |
![$\displaystyle \chi _{\mu \nu }\left( \bar{\Omega}\right) =\partial _{\lbrack \mu }\bar{ \theta}_{\nu ]},$](img877.png) |
(437) |
while the first-order reducibility relations (164) read as
 |
(438) |
 |
 |
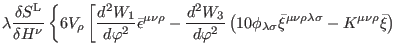 |
(439) |
| |
|
![$\displaystyle \left. -2\varepsilon _{\alpha \beta \gamma \delta \varepsilon }\f...
...
\frac{d^{2}W_{5}}{d\varphi ^{2}}\phi _{\lambda \sigma }\bar{\xi}\right]
\notag$](img881.png) |
(440) |
| |
|
 |
(441) |
| |
|
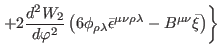 |
(442) |
| |
|
 |
(443) |
| |
|
![$\displaystyle \left. -2\varepsilon _{\alpha \beta \gamma \delta \varepsilon }\f...
...\sigma }\frac{
dW_{5}}{d\varphi }\phi _{\lambda \sigma }\bar{\xi}\right] \notag$](img885.png) |
(444) |
| |
|
 |
(445) |
| |
|
 |
(446) |
| |
|
 |
(447) |
| |
|
![$\displaystyle \left. +V_{\nu }\left( \frac{dW_{3}}{d\varphi }\bar{\xi}-2\vareps...
...d\varphi }\bar{\xi}
^{\alpha \beta \gamma \delta \varepsilon }\right) \right] ,$](img889.png) |
(448) |
 |
(449) |
 |
(459) |
Regarding the second-order reducibility, the transformations (165)
take the concrete form
such that the second-order reducibility relations (166) become
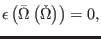 |
(466) |
 |
(467) |
 |
(468) |
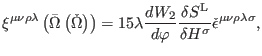 |
(469) |
 |
(470) |
Finally, we investigate the third-order reducibility, for which the
transformations (167) can be written as
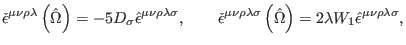 |
(471) |
while that the third-order reducibility relations (168) are listed
below
Ashkbiz Danehkar
2018-03-26
![]() and
and
![]() two independent sets of gauge parameters,
two independent sets of gauge parameters,