Let us consider the anti-Newtonian model (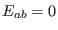 ) in a shearless
static
spacetime (
) in a shearless
static
spacetime (
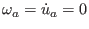 ) and a perfect-fluid model (
) and a perfect-fluid model (
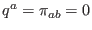 ). The constraints and propagations shall be
). The constraints and propagations shall be
![\begin{displaymath}\begin{array}[c]{cc} {C^{1}{}_{a}=-3\omega^{b}H_{ab}-{\textst...
...2}{}_{a}=(\mathrm{div}H)_{a}+\omega_{a}(\rho+p)=0,} \end{array}\end{displaymath}](img182.png) |
(77) |
![\begin{displaymath}\begin{array}[c]{cc} {P^{1}{}_{ab}=\mathrm{curl}(H)_{ab}=0,} ...
...b}-[\omega,H]_{\left\langle {ab}\right\rangle }=0,} \end{array}\end{displaymath}](img183.png) |
(78) |
![\begin{displaymath}\begin{array}[c]{cc} {C^{6}{}_{a}={\textstyle{\frac{2}{3}}}\m...
...ngle a\right. } \omega_{\left. b\right\rangle }=0.} \end{array}\end{displaymath}](img184.png) |
(79) |
To linearized order, divergence and evolution of Eq.
(78a) are
Equation (80) is consistent only in the spacetime being free
from either the gravitational mass and pressure or the gradient of
expansion. According to Eqs. (77) and
(79), the last term in Eq. (81) has to
vanish:
![$\displaystyle \mathrm{curl}([\omega,H])_{\left\langle {ab}\right\rangle }=0.$](img190.png) |
(82) |
It is a necessary condition for the consistent evolution of
propagation. This condition is satisfied with irrotational vorticity
products of gravitomagnetic, but it is not consistent with Eq.
(79b):
Thus, the anti-Newtonian model is generally inconsistent with
relativistic models. Furthermore, there is not a possibility of
gravitational waves.
Subsections
Ashkbiz Danehkar
2018-03-26
![]() ) in a shearless
static
spacetime (
) in a shearless
static
spacetime (
![]() ) and a perfect-fluid model (
) and a perfect-fluid model (
![]() ). The constraints and propagations shall be
). The constraints and propagations shall be