4 Gravitational Waves

We now obtain the temporal evolution of the dynamic propagations ( $P^{1,2} {}_{ab}$) in a perfect-fluid model ( $q^{a}=\pi_{ab}=0$):

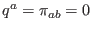$$C^{1}{}_{a}={(\mathrm{div}E)_{a}}-3\omega^{b}H_{ab}-[\sigma,H]_{a} -{\textstyle{\frac{1}{3}}}\mathrm{D}_{a}\rho=0,$$ (51)

$$C^{2}{}_{a}={(\mathrm{div}H)_{a}}+3\omega^{b}E_{ab}+[\sigma,E]_{a}+\omega _{a}(\rho+p)=0,$$ (52)

$$P^{1}{}_{ab}= \mathrm{curl}(H)_{ab}+2[\dot{u},H]_{\left\langle {ab}\right\rangl... ... {ab}\right\rangle }-\Theta E_{ab}+[\omega,E]_{\left\langle {ab}\right\rangle }$$

$$+3\sigma_{c\left\langle a\right. }E_{\left. b\right\rangle }{} ^{c}-{\textstyle{\frac{1}{2}}}\sigma_{ab}(\rho+p) =0,$$ (53)

$$P^{2}{}_{ab}= \mathrm{curl}(E)_{ab}+2[\dot{u},E]_{\left\langle {ab}\right\rangl... ... {ab}\right\rangle }+\Theta H_{ab}-[\omega,H]_{\left\langle {ab}\right\rangle }$$

$$-3\sigma_{c\left\langle a\right. }H_{\left. b\right\rangle }{}^{c}=0.$$ (54)

To the first order, the evolution of propagation is

$$\dot{P}^{1}{}_{ab}= \mathrm{D}^{2}E_{ab}-\ddot{E}_{\left\langle {ab} \right\rangle }-... ...gle }-{\textstyle{\frac{4}{3}}}\Theta P^{1} {}_{ab}+\mathrm{curl}(P^{2}){}_{ab}$$

$$-{\textstyle{\frac{4}{3}}}\Theta^{2}E_{ab}-{\textstyle{\frac{7}{3... ...e a\right. }\sigma_{\left. b\right\rangle }{}^{c}-\sigma _{cd}E^{cd}\sigma_{ab}$$

$$+E^{cd}\sigma_{ca}\sigma_{bd}-\sigma^{cd}\sigma_{c(a}E_{b)d}+\var... ...(a}\dot{E}_{b)}{}^{c}\omega^{d}+\varepsilon_{cd(a}E_{b)}{}^{c}\dot{\omega }^{d}$$

$$+{\textstyle{\frac{4}{3}}}\Theta\lbrack\omega,E]_{\left\langle {a... ...ga^{d} +3\dot{\sigma}_{c\left\langle a\right. }E_{\left. b\right\rangle }{}^{c}$$

$$+3\sigma_{c\left\langle a\right. }\dot{E}_{\left. b\right\rangle ... ...}{2}}} \mathrm{D}_{\left\langle a\right. }\omega^{c}H_{\left. b\right\rangle c}$$

$$-{\textstyle{\frac{3}{2}}}\mathrm{D}_{\left\langle a\right. }[\si... ...k\dot {u},H]_{\left\langle {ab}\right\rangle }+\mathrm{curl}([\omega,H])_{{ab}}$$

$$+3\mathrm{curl}\left( {\sigma_{c\left\langle a\right. }H_{\left. ... ...(a} \mathrm{D}^{e}H_{b)}{}^{d}+2\varepsilon_{cd(a}\dot{H}_{b)}{}^{c}\dot{u}^{d}$$

$$+2\varepsilon_{cd(a}H_{b)}{}^{c}\ddot{u}^{d}+2\dot{\varepsilon}_{... ...{b)} {}^{c}\dot{u}^{d}-{\textstyle{\frac{1}{2}}}\sigma_{ab}(\dot{\rho}+\dot{p})$$

$$-{\textstyle{\frac{1}{3}}}\Theta\sigma_{ab}(\rho+p) =0.$$ (55)

We neglect products of kinematic quantities with respect to the undisturbed metrics (unexpansive static spacetime). We can also prevent the perturbations that are merely associated with coordinate transformation, since they have no physical significance. In free space, we get

$$\dot{P}^{1}{}_{ab}=\mathrm{D}^{2}E_{ab}-\ddot{E}_{\left\langle {a... ... }-{\textstyle{\frac{4}{3}}}\Theta P^{1} {}_{ab}+\mathrm{curl}(P^{2}){}_{ab}=0.$$ (56)

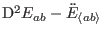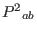To be consistent with Eqs. (51)-(54), $\mathrm{D} ^{2}E_{ab}-\ddot{E}_{\left\langle {ab}\right\rangle }$ has to vanish. Similarly, the evolution of $P^{2}{}_{ab}$ shows that $\mathrm{D}^{2} H_{ab}-\ddot{H}_{\left\langle {ab}\right\rangle }=0$. The evolutions reflect that the divergenceless and nonvanishing rotation of the Weyl fields are necessary conditions for gravitational waves:

$$\begin{array}[c]{cc} {(\mathrm{div}E)_{a}\mathrm{\ =}(\mathrm... ...{curl} (E){}_{ab}\neq0\neq\mathrm{curl}(H){}_{ab}.} \end{array}$$ (57)

Indeed, the rotation of the Weyl fields characterizes the wave solutions. The gravitomagnetic field is explicitly important to describe the gravitational waves, and is comparable with the Maxwell fields.

We use Eq. (18) to provide two more constraints:

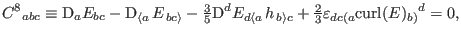$$C^{8}{}_{abc}\equiv\mathrm{D}_{a}E_{bc}-\mathrm{D}_{\left\langle ... ...e c}+{\textstyle{\frac {2}{3}}}\varepsilon_{dc(a}\mathrm{curl}(E)_{b)}{}^{d}=0,$$ (58)

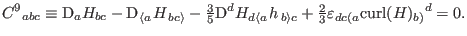$$C^{9}{}_{abc}\equiv\mathrm{D}_{a}H_{bc}-\mathrm{D}_{\left\langle ... ...e c}+{\textstyle{\frac {2}{3}}}\varepsilon_{dc(a}\mathrm{curl}(H)_{b)}{}^{d}=0.$$ (59)

To first order, divergence of Eq. (58) is

$$\mathrm{D}^{a}C^{8}{}_{abc}= \mathrm{D}^{2}E_{bc}-\mathrm{D}^{a}\mathrm{D} _{\left\langle a\ri... ...thrm{D}^{a}\mathrm{D}^{d}E_{d\left\langle a\right. }h_{\left. b\right\rangle c}$$

$$+{\textstyle{\frac{1}{3}}}\mathrm{D}^{a}\varepsilon_{dca}\mathrm{... ...yle{\frac{1}{3}}}\varepsilon_{dcb}\mathrm{D} ^{a}\mathrm{curl}(E)_{a}{}^{d} =0.$$ (60)

On substituting Eq. (54), it becomes

$$\mathrm{D}^{a}C^{8}{}_{abc}= \mathrm{D}^{2}E_{bc}-\mathrm{D}^{a}\mathrm{D} _{\left\langle a\ri... ...}{5}}}\mathrm{D}^{a}C^{1}{}_{\left\langle a\right. }h_{\left. b\right\rangle c}$$

$$+{\textstyle{\frac{2}{3}}}\mathrm{D}^{a}\varepsilon^{d}{}_{c(a}P^... ...}} \mathrm{D}^{a}[\sigma,H]_{\left\langle a\right. }h_{\left. b\right\rangle c}$$

$$-{\textstyle{\frac{1}{5}}}\mathrm{D}^{a}\mathrm{D}_{\left\langle ... ...rm{D}^{a}\varepsilon^{d}{}_{c(a}[\dot {u},E]_{\left\langle {b)d}\right\rangle }$$

$$-\Theta{\textstyle{\frac{2}{3}}}\mathrm{D}^{a}\varepsilon^{d}{}_{... ...hrm{D}^{a}\varepsilon^{d}{}_{c(a} [\omega,H]_{\left\langle {b)d}\right\rangle }$$

$$+2\mathrm{D}^{a}\varepsilon^{d}{}_{c(a}\sigma_{c\left\langle {b)}\right. }H_{\left. d\right\rangle }{}^{c} =0.$$ (61)

We abandon products of kinematic quantities in the undisturbed metrics:

$$\mathrm{D}^{a}C^{8}{}_{abc}= \mathrm{D}^{2}E_{bc}-\mathrm{D}^{a}\mathrm{D} _{\left\langle a\ri... ...}{5}}}\mathrm{D}^{a}C^{1}{}_{\left\langle a\right. }h_{\left. b\right\rangle c}$$

$$+{\textstyle{\frac{2}{3}}}\mathrm{D}^{a}\varepsilon^{d}{}_{c(a}P^{2}{} _{b)d}-{\textstyle{\frac{2}{3}}}\mathrm{curl}(\dot{H})_{ab} =0.$$ (62)

To linearized order, we get $\mathrm{curl}(S_{ab})^{\cdot}=\mathrm{curl} \dot{S}_{ab}$. Using the later point and the evolution of Eq. (53 ), we obtain:

$$\mathrm{D}^{a}C^{8}{}_{abc}= \mathrm{D}^{2}E_{bc}-\mathrm{D}^{a}\mathrm{D} _{\left\langle a\ri... ...t\rangle c}-{\textstyle{\frac{2}{3}}}\ddot{E}_{\left\langle {ab}\right\rangle }$$

$$-{\textstyle{\frac{3}{5}}}\mathrm{D}_{\left\langle a\right. }C^{1... ...silon^{d} {}_{c(a}P^{2}{}_{b)d}-{\textstyle{\frac{2}{3}}}\dot{P}^{1}{}_{ab} =0.$$ (63)

The result can be compared to the wave solution (56). Without the distortion parts, it is inconsistent with a generic description of wave. Distortion of the gravitoelectric field ( 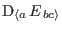$\mathrm{D}_{\left\langle a\right. }E_{\left. {bc}\right\rangle }$) must not vanish to provide the wave solution. We also obtain similar condition for the gravitomagnetic field. In free space, the divergence of the Weyl fields, determined by the matter, must be free. The temporal evolution decides that the rotation of the Weyl fields must be non-zero. Now, the distortion provides another condition to characterize the evolution of the Weyl fields:

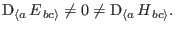$$\mathrm{D}_{\left\langle a\right. }E_{\left. {bc}\right\rangle }\neq 0\neq\mathrm{D}_{\left\langle a\right. }H_{\left. {bc}\right\rangle }.$$ (64)

The existence of rotation and distortion is necessary condition to maintain the wave solutions.