To provide the equations of motion, we use the Ricci
identities for the vector field  :
:
![$\displaystyle 2\nabla_{\lbrack a}\nabla_{b]}u_{c}=R_{abcd}u^{d}.$](img108.png) |
(44) |
We substitute the vector field  from the kinematic
quantities, using the Einstein equation, and separating out the
orthogonally projected part into trace, symmetric traceless, and
skew symmetric parts. We obtain constraints and propagations for the
kinematic quantities as follows[42]:
from the kinematic
quantities, using the Einstein equation, and separating out the
orthogonally projected part into trace, symmetric traceless, and
skew symmetric parts. We obtain constraints and propagations for the
kinematic quantities as follows[42]:
 |
(45) |
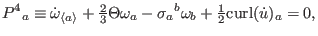 |
(46) |
Equation (45), called the Raychaudhuri propagation formula,
is the basic equation of gravitational attraction.[45]
In Eq. (46), the evolution of vorticity is conserved by
the rotation of acceleration. Equation (47) shows that the
gravitoelectric field is propagated in shear, vorticity,
acceleration, and anisotropic stress.
The Ricci identities also provide a set of constraints:
 |
(48) |
![$\displaystyle C^{6}{}_{a}\equiv{\textstyle{\frac{2}{3}}}\mathrm{D}_{a}\Theta-{(...
...hrm{div} \sigma)_{a}}+\mathrm{curl}(\omega)_{a}+2[\dot{u},\omega]_{a}-q_{a} =0,$](img115.png) |
(49) |
 |
(50) |
Equation (48) presents the divergence of vorticity. Equation
(49) links the divergence of shear to the rotation of
vorticity. Equation (50) characterizes the gravitomagnetic
field as the distortion of vorticity and the rotation of shear.
Ashkbiz Danehkar
2018-03-26
![]() :
: