5.1 Newtonian Model

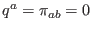Let us consider the Newtonian model ($H_{ab}=0$) in an irrotational static spacetime ( $\omega_{a}=\dot{u}_{a}=0$) and a perfect-fluid model ( $q^{a}=\pi_{ab}=0$). The constraints and propagations shall be

$$\begin{array}[c]{cc} {C^{1}{}_{a}=(\mathrm{div}E)_{a}-{\texts... ... \rho=0,} & {~~~~~~~~C^{2}{}_{a}=[\sigma,E]_{a}=0,} \end{array}$$ (65)

$$\begin{array}[c]{c} {P^{1}{}_{ab}=-\dot{E}_{\left\langle {ab}... ...p)=0,}\\ \\ {P^{2}{}_{ab}=\mathrm{curl}(E)_{ab}=0,} \end{array}$$ (66)

$$\begin{array}[c]{cc} {C^{6}{}_{a}={\textstyle{\frac{2}{3}}}\m... ...~~~~~~~C^{7}{}_{ab}=-\mathrm{curl}(\sigma)_{ab}=0.} \end{array}$$ (67)

To first order, divergence and evolution of Eq. (66b) are

$$\mathrm{D}^{b}P^{2}{}_{ab} = {\textstyle{\frac{1}{2}}}\varepsilon _{abc}\mathrm{D}^{b}\mathrm{... ...+{\textstyle{\frac{1}{3}}} \Theta\lbrack\sigma,E]_{a}-\sigma_{ab}[\sigma,E]^{b}$$

$$= {\textstyle{\frac{1}{2}}}\mathrm{curl}(C^{1}){}_{a}+{\textstyle{\... ...}-\sigma_{a}{}^{b}C^{2}{}_{b}+{\textstyle{\frac{1} {3}}}\omega{}_{a}\dot{\rho},$$ (68)

$$\dot{P}^{2}{}_{ab} = -{\textstyle{\frac{1}{3}}}\Theta{\mathrm{curl} (E)_{ab}}-\sigma_{... ...c}\varepsilon_{cd(a}\mathrm{D}^{e}E_{b)}{} ^{d}+{\mathrm{curl}(\dot{E})}_{{ab}}$$

$$= -{\textstyle{\frac{3}{2}}}\varepsilon^{cd}{}_{(a}\sigma_{b)c}C^{1... ...}_{ab}+{\textstyle{\frac{3}{2}} }\varepsilon^{c}{}_{d(a}C^{6}{}_{c}E_{b)}{}^{d}$$

$$-{\textstyle{\frac{1}{2}}}(\rho+p)C^{7}{}_{ab}-\mathrm{curl}(P^{1... ...mathrm{curl(}\sigma_{c\left\langle a\right. }E_{\left. b\right\rangle }{}^{c}).$$ (69)

The last parameter ( ${\textstyle{\frac{1}{3}}}\omega_{a}\dot{\rho}$) in Eq. (68) vanishes because of irrotational condition. Equation (68) then conserves the constraints. Equation (69) must be consistent with Eqs. (65) and (67). Thus, the last parameters in Eq. (69) has to vanish:

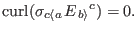$$\mathrm{curl}(\sigma_{c\left\langle a\right. }E_{\left. b\right\rangle } {}^{c})=0.$$ (70)

It is a necessary condition for the consistent evolution of propagation. This condition is satisfied with irrotational product of gravitoelectric and shear, but it is a complete contrast to Eq. (65b). Thus, the Newtonian model is generally inconsistent with generic relativistic models. Moreover, the temporal evolution of propagation shows no wave solutions.