7 The coupled theory: Lagrangian and gauge structure
In this section we start from the concrete form of (151) and
identify the entire gauge structure of the Lagrangian model that describes
all consistent interactions in  between the BF theory and the massless
tensor field
between the BF theory and the massless
tensor field
 . To this end we recall the discussion
from the end of section 2 related to the relationship between the
gauge structure of a given Lagrangian field theory and various terms of
definite antighost number present in the solution of the master equation. Of
course, we assume that the functions
. To this end we recall the discussion
from the end of section 2 related to the relationship between the
gauge structure of a given Lagrangian field theory and various terms of
definite antighost number present in the solution of the master equation. Of
course, we assume that the functions
 ,
,  together with the constants
together with the constants  and
and  satisfy
equations (130)-(135) and (141)-(142). The
analysis of solutions that are interesting from the point of view of
cross-couplings (at least one of the constants
satisfy
equations (130)-(135) and (141)-(142). The
analysis of solutions that are interesting from the point of view of
cross-couplings (at least one of the constants  and
and  is
nonvanishing) is done in Section 8.
is
nonvanishing) is done in Section 8.
The piece of antighost number zero from (151) provides
nothing but the Lagrangian action of the interacting theory
![$\displaystyle S^{\mathrm{L}}\left[ \Phi ^{\alpha _{0}}\right]$](img422.png) |
 |
![$\displaystyle \int d^{5}x\left\{ H_{\mu
}\partial ^{\mu }\varphi +\tfrac{1}{2}B...
...{1}{3}K^{\mu \nu \rho }\partial _{\lbrack \mu }\phi _{\nu
\rho ]}\right. \notag$](img423.png) |
(179) |
| |
|
![$\displaystyle +\lambda \left[ W_{1}V_{\mu }H^{\mu }+W_{2}B_{\mu \nu }\phi ^{\mu...
... _{\lbrack \mu \nu }V_{\rho ]}K^{\mu \nu \rho }+\bar{M}(\varphi
)\right. \notag$](img424.png) |
(180) |
| |
|
![$\displaystyle \left. +\varepsilon ^{\alpha \beta \gamma \delta \varepsilon }\le...
...on
}+W_{6}B_{\alpha \beta }K_{\gamma \delta \varepsilon }\right) \right] \notag$](img425.png) |
(181) |
| |
|
 |
(182) |
| |
|
![$\displaystyle \left. +\lambda \left( k_{1}\phi ^{\mu \nu }-\tfrac{k_{2}}{20}\ti...
...phi
_{\mu \nu }-\tfrac{k_{2}}{20}\tilde{K}_{\mu \nu }\right) \right] \right\} ,$](img427.png) |
(183) |
where
 is the field spectrum (2). The terms of
antighost number one from the deformed solution of the master equation,
generically written as
is the field spectrum (2). The terms of
antighost number one from the deformed solution of the master equation,
generically written as
 , allow the identification of the
gauge transformations of action (152) via replacing the ghosts
, allow the identification of the
gauge transformations of action (152) via replacing the ghosts
 with the gauge parameters
with the gauge parameters
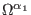
 |
(184) |
In our case, taking into account formula (151) and
maintaining the notation (8) for the gauge parameters, we find
the concrete form of the deformed gauge transformations as
 |
(185) |
 |
 |
 |
(186) |
| |
|
 |
(187) |
| |
|
 |
(188) |
| |
|
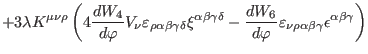 |
(189) |
| |
|
 |
(190) |
| |
|
![$\displaystyle \left. -\frac{dW_{5}}{d\varphi }\phi _{\nu \rho }\left( V_{\lambda }\xi
_{\sigma }-\tfrac{1}{4}\phi _{\lambda \sigma }\epsilon \right) \right] ,$](img439.png) |
(191) |
 |
(192) |
![$\displaystyle \bar{\delta}_{\Omega }t_{\mu \nu \vert\alpha }=\partial _{\lbrack...
...{\nu ]\beta \gamma \delta \varepsilon }\xi ^{\beta \gamma \delta \varepsilon },$](img450.png) |
(199) |
where, in addition, we used the notations
 |
(200) |
We observe that the cross-interaction terms,
are only of order one in the deformation parameter and couple the tensor
field
 to the two-form
to the two-form
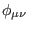 and to
the three-form
and to
the three-form
 from the BF sector. Also, it is
interesting to see that the interaction components
from the BF sector. Also, it is
interesting to see that the interaction components
which describe self-interactions in the BF sector, are strictly due to the
presence of the tensor
 (in its absence
(in its absence
 , so they would vanish). The gauge transformations of the BF
fields
, so they would vanish). The gauge transformations of the BF
fields
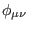 and
and
 are deformed in such a way
to include gauge parameters from the
are deformed in such a way
to include gauge parameters from the  sector. Related to the other BF
fields,
sector. Related to the other BF
fields,  ,
,  ,
,  , and
, and
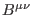 , their gauge
transformations are also modified with respect to the free theory, but only
with terms specific to the BF sector. A remarkable feature is that the gauge
transformations of the tensor
, their gauge
transformations are also modified with respect to the free theory, but only
with terms specific to the BF sector. A remarkable feature is that the gauge
transformations of the tensor
 are modified by
shift terms in some of the gauge parameters from the BF sector.
are modified by
shift terms in some of the gauge parameters from the BF sector.
From the components of higher antighost number present in (151
) we read the entire gauge structure of the interacting theory: the
commutators among the deformed gauge transformations (154)-(160), and hence the properties of the deformed gauge algebra, their
associated higher-order structure functions, and also the new reducibility
functions and relations together with their properties. (The reducibility
order itself of the interacting theory is not modified by the deformation
procedure and remains equal to that of the free model, namely, three.) We do
not give here the concrete form of all these deformed structure functions,
which is analyzed in detail in Appendix F, but only briefly
discuss their main properties by contrast to the gauge features of the free
theory (see section 2).
The nonvanishing commutators among the deformed gauge transformations result
from the terms quadratic in the ghosts with pure ghost number one present in
(151). Since their form can be generically written as
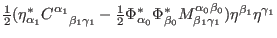 , it follows that the commutators among the deformed gauge
transformations only close on-shell (on the stationary surface of the
deformed field equations)
, it follows that the commutators among the deformed gauge
transformations only close on-shell (on the stationary surface of the
deformed field equations)
 |
(201) |
Here,
 stand for the
Euler-Lagrange (EL) derivatives of the interacting action (152),
stand for the
Euler-Lagrange (EL) derivatives of the interacting action (152),
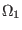 and
and
 represent two independent sets of gauge
parameters of the type (8), and
represent two independent sets of gauge
parameters of the type (8), and  is a quadratic
combination of
is a quadratic
combination of
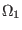 and
and
 . The exact form of the
corresponding commutators is included in the Appendix F (see
formulas (287)-(293)). In conclusion, the gauge algebra
corresponding to the interacting theory is open (the commutators among the
deformed gauge transformations only close on-shell), by contrast to the free
theory, where the gauge algebra is Abelian.
. The exact form of the
corresponding commutators is included in the Appendix F (see
formulas (287)-(293)). In conclusion, the gauge algebra
corresponding to the interacting theory is open (the commutators among the
deformed gauge transformations only close on-shell), by contrast to the free
theory, where the gauge algebra is Abelian.
The first-order reducibility functions and relations follow from the terms
linear in the ghosts for ghosts appearing in (151). Because
they can be generically set in the form (
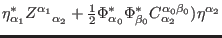 , it follows that if we transform the gauge parameters
, it follows that if we transform the gauge parameters
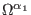 in terms of the first-order reducibility parameters
in terms of the first-order reducibility parameters
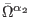 as in
as in
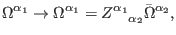 |
(202) |
then the transformed gauge transformations (153) of all fields
vanish on-shell
 |
(203) |
Along the same line, the second-order reducibility functions and relations
are given by the terms linear in the ghosts for ghosts for ghosts appearing
in (151), which can be generically written as
 . Consequently, if we transform the first-order
reducibility parameters
. Consequently, if we transform the first-order
reducibility parameters
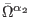 in terms of the
second-order reducibility parameters
in terms of the
second-order reducibility parameters
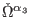 as in
as in
 |
(204) |
then the transformed gauge parameters (163) vanish on-shell
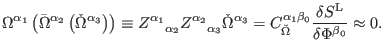 |
(205) |
Finally, the third-order reducibility functions and relations are withdrawn
from the terms linear in the ghosts for ghosts for ghosts for ghosts from (
151), which have the generic form
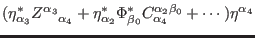 , such that if we transform the second-order reducibility parameters
, such that if we transform the second-order reducibility parameters
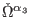 in terms of the third-order reducibility
parameters
in terms of the third-order reducibility
parameters
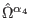 as in
as in
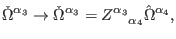 |
(206) |
then the transformed first-order reducibility parameters (165)
again vanish on-shell
 |
(207) |
In the above the notations
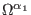 ,
,
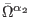 ,
,
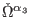 , and
, and
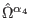 are
the same from the free case, namely (8), (16), (20), and (23), while the BRST generators are structured
according to formulas (25)-(31). It is now clear that the
reducibility relations associated with the interacting model ((164
), (166), and (168)) only hold on-shell, by contrast to
those corresponding to the free theory ((10), (12), and
respectively (14)), which hold off-shell. Their concrete form is
detailed in Appendix F.
are
the same from the free case, namely (8), (16), (20), and (23), while the BRST generators are structured
according to formulas (25)-(31). It is now clear that the
reducibility relations associated with the interacting model ((164
), (166), and (168)) only hold on-shell, by contrast to
those corresponding to the free theory ((10), (12), and
respectively (14)), which hold off-shell. Their concrete form is
detailed in Appendix F.
Ashkbiz Danehkar
2018-03-26
![]() between the BF theory and the massless
tensor field
between the BF theory and the massless
tensor field
![]() . To this end we recall the discussion
from the end of section 2 related to the relationship between the
gauge structure of a given Lagrangian field theory and various terms of
definite antighost number present in the solution of the master equation. Of
course, we assume that the functions
. To this end we recall the discussion
from the end of section 2 related to the relationship between the
gauge structure of a given Lagrangian field theory and various terms of
definite antighost number present in the solution of the master equation. Of
course, we assume that the functions
![]() ,
, ![]() together with the constants
together with the constants ![]() and
and ![]() satisfy
equations (130)-(135) and (141)-(142). The
analysis of solutions that are interesting from the point of view of
cross-couplings (at least one of the constants
satisfy
equations (130)-(135) and (141)-(142). The
analysis of solutions that are interesting from the point of view of
cross-couplings (at least one of the constants ![]() and
and ![]() is
nonvanishing) is done in Section 8.
is
nonvanishing) is done in Section 8.
![]() , it follows that the commutators among the deformed gauge
transformations only close on-shell (on the stationary surface of the
deformed field equations)
, it follows that the commutators among the deformed gauge
transformations only close on-shell (on the stationary surface of the
deformed field equations)
![]() , it follows that if we transform the gauge parameters
, it follows that if we transform the gauge parameters
![]() in terms of the first-order reducibility parameters
in terms of the first-order reducibility parameters
![]() as in
as in