In the theory of general relativity, we describe the local nature of
gravitational field nearby matter as an algebraic relation between
the Ricci curvature and the matter fields, i.e., the
Einstein field equations:
 |
(26) |
where  is the Ricci curvature,
is the Ricci curvature, 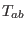 the energy-momentum
of the matter fields, and
the energy-momentum
of the matter fields, and
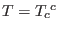 the trace of the
energy-momentum tensor.
the trace of the
energy-momentum tensor.
The successive contractions of Eq. (26) on using of Eq.
(24) lead to a set of relations:
![\begin{displaymath}\begin{array}[c]{cc} {R_{ab}u^{a}u^{b}={\textstyle{\frac{1}{2...
...style{\frac{1}{2}} }(\rho-p)h_{ab}+\pi_{ab},} & { } \end{array}\end{displaymath}](img67.png) |
(27) |
![\begin{displaymath}\begin{array}[c]{ccc} {R=R_{a}{}^{a},} & {~~~~~~~~T=T_{a}{}^{a}=-\rho+3p,} & {~~~~~~~~R=-T,} \end{array}\end{displaymath}](img68.png) |
(28) |
where 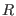 is the Ricci scalar. The Ricci curvature is derived from
the once contracted Riemann curvature tensor:
is the Ricci scalar. The Ricci curvature is derived from
the once contracted Riemann curvature tensor:
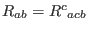 .
.
The Riemann tensor is split into symmetric (massless) traceless
 and traceful massive
and traceful massive  parts:
parts:
 |
(29) |
The symmetric traceless part of the Riemann curvature is called the
Weyl conformal curvature with the following properties:
![\begin{displaymath}\begin{array}[c]{cc} {C_{abcd}=C_{[ab][cd]},} & {~~~~~~~~C^{a}{}_{bca}=0=C_{a[bcd]}.} \end{array}\end{displaymath}](img74.png) |
(30) |
The nonlocal (long-range) fields, the parts of the curvature not
directly determined locally by matter, are given by the Weyl
curvature; propagating the Newtonian (and anti-Newtonian) forces and
gravitational waves. It can be shown that the Weyl tensor  is irreducibly split into the Newtonian
is irreducibly split into the Newtonian
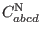 and
the anti-Newtonian
and
the anti-Newtonian
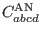 parts:
parts:
 |
(31) |
![$\displaystyle C_{\mathrm{N}}^{ab}{}_{cd}=4\{u^{[a}u_{[c}+h^{[a}{}_{[c}\}E^{b]}{}_{d]},$](img78.png) |
(32) |
![$\displaystyle C_{abcd}^{\mathrm{AN}}=2\varepsilon_{abe}u_{[c}H_{d]}{}^{e}+2\varepsilon _{cde}u_{[a}H_{b]}{}^{e},$](img79.png) |
(33) |
where
 is the gravitoelectric field and
is the gravitoelectric field and
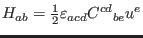 the gravitomagnetic field. They are spacelike and traceless
symmetric.
the gravitomagnetic field. They are spacelike and traceless
symmetric.
The traceful massive part of the Riemann curvature consists of the
matter fields and the characteristics of local interactions with
matter
Therefore, the Weyl curvature is linked to the matter fields through
the Riemann curvature.
Subsections
Ashkbiz Danehkar
2018-03-26
![]() and traceful massive
and traceful massive ![]() parts:
parts: