Anticipating constant profile solutions, we shall consider Eqs. (9
)-(12) in a stationary frame traveling at a constant normalized
velocity 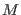 (to be referred to as the Mach number), implying the
transformation
(to be referred to as the Mach number), implying the
transformation 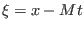 . The space and time derivatives are thus replaced by
. The space and time derivatives are thus replaced by
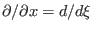 and
and
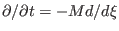 , respectively,
so Eqs. (9)-(12) take the form:
, respectively,
so Eqs. (9)-(12) take the form:
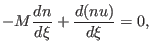 |
(21) |
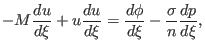 |
(22) |
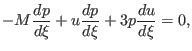 |
(23) |
![$\displaystyle \frac{d^{2}\phi}{d\xi^{2}}=-(\beta+1)+n+\beta\left[ 1-\frac{\phi} {(\kappa-\tfrac{3}{2})}\right] ^{-\kappa+1/2}.$](img149.png) |
(24) |
We assume that the equilibrium state is reached at both infinities
(
 ). Accordingly, we integrate and apply the boundary
conditions
). Accordingly, we integrate and apply the boundary
conditions  ,
, 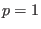 ,
,  and
and 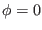 at
at 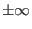 . One thus obtains
. One thus obtains
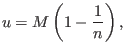 |
(25) |
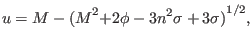 |
(26) |
and
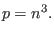 |
(27) |
Combining Eqs. (25)-(27), we obtain the following
biquadratic equation for the cool electron density,
 |
(28) |
The solution of Eq. (28) may be written as
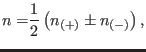 |
(29) |
where
From the boundary conditions,  at
at 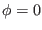 , it follows that the negative
sign must be taken in Eq. (29). Furthermore, we shall assume that
, it follows that the negative
sign must be taken in Eq. (29). Furthermore, we shall assume that
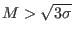 , i.e., that the cool electrons are supersonic, while the
hot electrons are subsonic, thus we require that
, i.e., that the cool electrons are supersonic, while the
hot electrons are subsonic, thus we require that 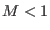 .
.
Reality of the density variable imposes the requirement
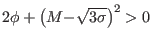 , which implies a limit
on the electrostatic potential value
, which implies a limit
on the electrostatic potential value
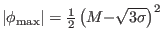 associated with negative solitary structures (positive electric potentials,
should they exist, satisfy the latter condition automatically, and are thus
not limited).
associated with negative solitary structures (positive electric potentials,
should they exist, satisfy the latter condition automatically, and are thus
not limited).
Substituting the density expression (29)-(31) into
Poisson's equation (24) and integrating,
yields the pseudo-energy balance equation for a unit mass in a conservative
force field, if one defines 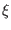 as ``time''
and
as ``time''
and 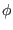 as ``position'' variable:
as ``position'' variable:
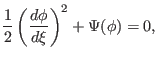 |
(32) |
where the Sagdeev pseudopotential
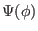 is given by
is given by
Figure 2:
(Color online) Variation of the lower limit  (lower curves)
and the upper limit
(lower curves)
and the upper limit  (upper curves) with the hot-to-cold electron
density ratio
(upper curves) with the hot-to-cold electron
density ratio  for different values of the temperature ratio
for different values of the temperature ratio 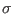 .
Solitons may exist for values of the Mach number
.
Solitons may exist for values of the Mach number 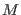 in the region between the
lower and the upper curve(s) of the same style/color. Curves: (a-b)
in the region between the
lower and the upper curve(s) of the same style/color. Curves: (a-b)
 (solid),
(solid),  (dashed), and
(dashed), and 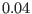 (dot-dashed), and (c)
(dot-dashed), and (c)
 (solid),
(solid), 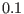 (dashed), and
(dashed), and  (dot-dashed) Here, we have
taken: (a)
(dot-dashed) Here, we have
taken: (a) 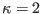 , (b)
, (b)
 (quasi-Maxwellian), and (c)
(quasi-Maxwellian), and (c)
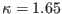 .
.
|
|
Figure 3:
(Color online) Variation of the lower limit 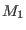 (lower curves)
and the upper limit
(lower curves)
and the upper limit  (upper curves) with the suprathermality parameter
(upper curves) with the suprathermality parameter
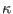 for different values of the temperature ratio
for different values of the temperature ratio 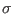 (upper panel),
and density ratio
(upper panel),
and density ratio  (bottom panel). Solitons may exist for values of the
Mach number
(bottom panel). Solitons may exist for values of the
Mach number 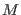 in the region between the lower and upper curves of the same
style/color. Upper panel:
in the region between the lower and upper curves of the same
style/color. Upper panel:
 (solid curve),
(solid curve),  (dashed), and
(dashed), and
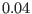 (dot-dashed). Here, we have taken
(dot-dashed). Here, we have taken 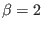 . Lower panel:
. Lower panel:
 (solid),
(solid),  (dashed),
(dashed),  (dot-dashed), and
(dot-dashed), and  (solid circles).
Here,
(solid circles).
Here,
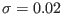 .
.
|
|
Ashkbiz Danehkar
2018-03-28
![]() (to be referred to as the Mach number), implying the
transformation
(to be referred to as the Mach number), implying the
transformation ![]() . The space and time derivatives are thus replaced by
. The space and time derivatives are thus replaced by
![]() and
and
![]() , respectively,
so Eqs. (9)-(12) take the form:
, respectively,
so Eqs. (9)-(12) take the form:
![$\displaystyle {\equiv}\left[ \dfrac{{2\phi+}\left( {M+}\sqrt{3{\sigma} }\right) ^{2}}{3{\sigma}}\right] ^{1/2},$](img162.png)
![$\displaystyle {\equiv}\left[ \dfrac{{2\phi+\left( {M-}\sqrt{3{\sigma}}\right) ^{2}}}{3{\sigma}}\right] ^{1/2}.$](img164.png)
![]() , which implies a limit
on the electrostatic potential value
, which implies a limit
on the electrostatic potential value
![]() associated with negative solitary structures (positive electric potentials,
should they exist, satisfy the latter condition automatically, and are thus
not limited).
associated with negative solitary structures (positive electric potentials,
should they exist, satisfy the latter condition automatically, and are thus
not limited).
![]() as ``time''
and
as ``time''
and ![]() as ``position'' variable:
as ``position'' variable:
![\includegraphics[
height=4.6406in,
width=2.4664in
]{figures/fig2.eps}](img175.png)
![\includegraphics[
height=3.3122in,
width=2.6792in
]{figures/fig3.eps}](img176.png)