- ... Bizdadea1
- E-mail address: bizdadea@central.ucv.ro
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Cioroianu2
-
E-mail address: manache@central.ucv.ro
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Danehkar3
-
Present address: School of Mathematics and Physics, Queen's University,
Belfast BT7 1NN, UK. E-mail address: adanehkar01@qub.ac.uk
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Saliu4
-
E-mail address: osaliu@central.ucv.ro
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...araru5
-
E-mail address: scsararu@central.ucv.ro
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... theories.6
-
Decomposition (87) does not include a component responsible for the
self-interactions of the tensor field with the mixed symmetry
 since
any such component has been proved in [62] to be trivial.
since
any such component has been proved in [62] to be trivial.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... as7
-
In principle, one can add to
 the terms
the terms
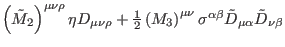 , where
, where
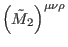 is
the Hodge dual of an expression similar to (85) with
is
the Hodge dual of an expression similar to (85) with
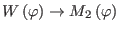 , and
, and
 reads as in (85) with
reads as in (85) with
 . Both
. Both  and
and  are some arbitrary, real, smooth functions depending on the undifferentiated
scalar field. It can be shown that the above terms finally lead to trivial
interactions, so they can be removed from the first-order deformation.
are some arbitrary, real, smooth functions depending on the undifferentiated
scalar field. It can be shown that the above terms finally lead to trivial
interactions, so they can be removed from the first-order deformation.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... as8
-
In principle, one can add to
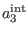 the term
the term
 , where
, where
 reads as in (84), with
reads as in (84), with
 . It is possible to
show that such a term outputs only trivial deformations.
. It is possible to
show that such a term outputs only trivial deformations.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.