C. No-go result for  in
in
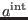
We have seen in the previous two Appendixes A and B that we
can always take (193) and (204) in (181). Consequently,
the first-order deformation of the solution to the master equation in the
interacting case stops at antighost number three
 |
(280) |
where the components on the right-hand side of (205) are subject to
the equations (68) and (66)-(67) for  .
.
The piece
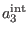 as solution to equation (68) for
as solution to equation (68) for  has the general form expressed by (75) for
has the general form expressed by (75) for  , with
, with
 from
from
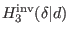 . Looking at formula (76)
and also at relation (81) in antighost number three and
requiring that
. Looking at formula (76)
and also at relation (81) in antighost number three and
requiring that
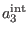 mixes BRST generators from the BF and
mixes BRST generators from the BF and  sectors, we find that the most general solution to (68) for
sectors, we find that the most general solution to (68) for  reads as8
reads as8
where any object denoted by  represents an arbitrary, real constant.
Inserting (206) in equation (66) for
represents an arbitrary, real constant.
Inserting (206) in equation (66) for  and using
definitions (35)-(52), we can write
and using
definitions (35)-(52), we can write
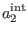 |
 |
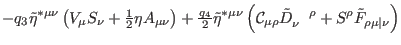 |
(284) |
| |
|
 |
(285) |
| |
|
 |
(286) |
| |
|
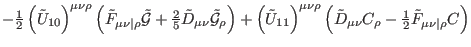 |
(287) |
| |
|
 |
(288) |
The component
 represents the solution to the
homogeneous equation in antighost number two (68) for
represents the solution to the
homogeneous equation in antighost number two (68) for 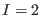 , so
, so
 is a nontrivial element from
is a nontrivial element from
 of pure ghost number two and antighost number two. It is useful to decompose
of pure ghost number two and antighost number two. It is useful to decompose
 as a sum between two terms
as a sum between two terms
 |
(289) |
with
 the solution to (68) for
the solution to (68) for 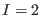 that
ensures the consistency of
that
ensures the consistency of
 in antighost number one,
namely the existence of
in antighost number one,
namely the existence of
 as solution to (67)
for
as solution to (67)
for  with respect to the terms from
with respect to the terms from
 containing
the functions of the type
containing
the functions of the type  or the constants denoted by
or the constants denoted by  , and
, and
 the solution to (68) for
the solution to (68) for 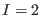 that is
independently consistent in antighost number one
that is
independently consistent in antighost number one
 |
(290) |
Using definitions (35)-(49) and decomposition (208
), by direct computation we obtain that
where we used the notations
 |
 |
 |
(293) |
| |
|
![$\displaystyle \left. +\tfrac{q_{5}}{4}\sigma _{\lambda \sigma }\left( D_{\mu \a...
...ha \lambda }\right) \tilde{F}_{\quad \vert\rho }^{\beta \sigma }
\right] \notag$](img628.png) |
(294) |
| |
|
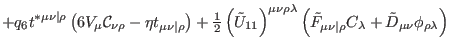 |
(295) |
| |
|
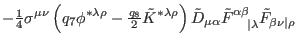 |
(296) |
| |
|
 |
(297) |
| |
|
 |
(298) |
| |
|
 |
(299) |
and
 are some local currents. It is easy to see that
are some local currents. It is easy to see that  given in (212) is a nontrivial object from
given in (212) is a nontrivial object from
 in pure ghost number two, which obviously does not reduce to a
full divergence. Then, since (210) requires that it is
in pure ghost number two, which obviously does not reduce to a
full divergence. Then, since (210) requires that it is  -exact modulo
-exact modulo  , it must vanish, which further implies that all the
functions of the type
, it must vanish, which further implies that all the
functions of the type
 are some real constants and
all the constants denoted by
are some real constants and
all the constants denoted by  vanish
vanish
Inserting conditions (213) and (214) into (206),
we conclude that we conclude that we can safely take
 |
(306) |
in (205).
Ashkbiz Danehkar
2018-03-26
![]() as solution to equation (68) for
as solution to equation (68) for ![]() has the general form expressed by (75) for
has the general form expressed by (75) for ![]() , with
, with
![]() from
from
![]() . Looking at formula (76)
and also at relation (81) in antighost number three and
requiring that
. Looking at formula (76)
and also at relation (81) in antighost number three and
requiring that
![]() mixes BRST generators from the BF and
mixes BRST generators from the BF and ![]() sectors, we find that the most general solution to (68) for
sectors, we find that the most general solution to (68) for ![]() reads as8
reads as8