5 Computation of first-order deformation
In the case  the nonintegrated density of the first-order deformation
(see (64)) becomes
the nonintegrated density of the first-order deformation
(see (64)) becomes
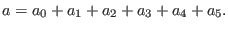 |
(97) |
We can further decompose  in a natural manner as a sum between two kinds
of deformations
in a natural manner as a sum between two kinds
of deformations
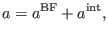 |
(98) |
where
 contains only fields/ghosts/antifields from the BF
sector and
contains only fields/ghosts/antifields from the BF
sector and
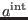 describes the cross-interactions between the
two theories.6 The piece
describes the cross-interactions between the
two theories.6 The piece
 is completely known [32]. It is parameterized
by seven smooth, but otherwise arbitrary functions of the undifferentiated
scalar field,
is completely known [32]. It is parameterized
by seven smooth, but otherwise arbitrary functions of the undifferentiated
scalar field,
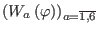 and
and
 . In the sequel we analyze the cross-interacting
piece,
. In the sequel we analyze the cross-interacting
piece,
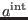 .
.
Due to the fact that
 and
and
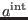 involve
different types of fields and that
involve
different types of fields and that
 separately satisfies an
equation of the type (62), it follows that
separately satisfies an
equation of the type (62), it follows that
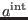 is
subject to the equation
is
subject to the equation
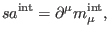 |
(99) |
for some local current
 . In the sequel we determine
the general solution to (88) that complies with all the hypotheses
mentioned in the beginning of section 4.
. In the sequel we determine
the general solution to (88) that complies with all the hypotheses
mentioned in the beginning of section 4.
In agreement with (86), the general solution to the equation
 can be chosen to stop
at antighost number
can be chosen to stop
at antighost number 
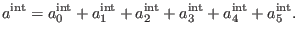 |
(100) |
We will show in Appendixes A, B and C that we can
always take
 into decomposition (89), without loss of nontrivial
contributions. Consequently, the first-order deformation of the solution to
the master equation in the interacting case can be taken to stop at
antighost number two
into decomposition (89), without loss of nontrivial
contributions. Consequently, the first-order deformation of the solution to
the master equation in the interacting case can be taken to stop at
antighost number two
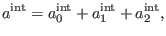 |
(101) |
where the components on the right-hand side of (90) are subject to
equations (68) and (66)-(67) for  .
.
The piece
 as solution to equation (68) for
as solution to equation (68) for  has the general form expressed by (75) for
has the general form expressed by (75) for 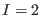 , with
, with
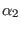 from
from
 . Looking at formula (76)
and also at relation (81) in antighost number two and requiring
that
. Looking at formula (76)
and also at relation (81) in antighost number two and requiring
that
 mixes BRST generators from the BF and
mixes BRST generators from the BF and  sectors, we get that the most general solution to (68) for
sectors, we get that the most general solution to (68) for 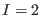 reads as7
reads as7
where all quantities denoted by  or
or  are some real, arbitrary
constants.
are some real, arbitrary
constants.
In the above and from now on we will use a compact writing in terms of the
Hodge duals
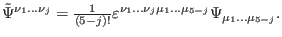 |
(104) |
Consequently
 ,
,
 and
and
 are the Hodge duals of
are the Hodge duals of
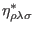 ,
,
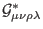 , and respectively
, and respectively
 .
.
Substituting (91) in (66) for 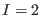 and using definitions (
35)-(52), we determine the solution
and using definitions (
35)-(52), we determine the solution
 under the form
under the form
where
 is the Hodge dual of
is the Hodge dual of
 defined in (3) with respect to its
first three indices
defined in (3) with respect to its
first three indices
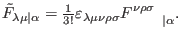 |
(108) |
In the last formulas
 is the dual of the
three-form
is the dual of the
three-form
 from action (1),
from action (1),
 and
and
 represent the duals
of the antifields
represent the duals
of the antifields
 and respectively
and respectively
 from (28).
from (28).
In the above
 is the solution to the homogeneous
equation (68) in antighost number one, meaning that
is the solution to the homogeneous
equation (68) in antighost number one, meaning that
 is a nontrivial object from
is a nontrivial object from
 in pure
ghost number one and in antighost number one. It is useful to decompose
in pure
ghost number one and in antighost number one. It is useful to decompose
 like in (208)
like in (208)
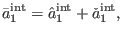 |
(109) |
with
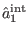 the solution to (68) for
the solution to (68) for  that
ensures the consistency of
that
ensures the consistency of
 in antighost number zero,
namely the existence of
in antighost number zero,
namely the existence of
 as solution to (67)
for
as solution to (67)
for  with respect to the terms from
with respect to the terms from
 containing
the constants of the type
containing
the constants of the type  or
or  , and
, and
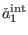 the
solution to (68) for
the
solution to (68) for  that is independently consistent in
antighost number zero
that is independently consistent in
antighost number zero
 |
(110) |
With the help of definitions (35)-(52) and taking into
account decomposition (208), we infer by direct computation
where
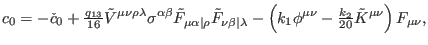 |
(113) |
and
 are some local currents. In the above
are some local currents. In the above
 and
and
 represent the
Hodge duals of the one-form
represent the
Hodge duals of the one-form
 and respectively of the two-form
and respectively of the two-form
 from (2) and
from (2) and
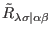 is nothing but the Hodge dual of the tensor
is nothing but the Hodge dual of the tensor
 defined in (72) with respect to its
first three indices, namely
defined in (72) with respect to its
first three indices, namely
 |
(118) |
Inspecting (97), we observe that equation (67) for  possesses solutions if and only if
possesses solutions if and only if  expressed by (99) is
expressed by (99) is
 -exact modulo
-exact modulo  . A straightforward analysis of
. A straightforward analysis of  shows
that this is not possible unless
shows
that this is not possible unless
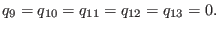 |
(119) |
Now, we insert conditions (101) in (91) and identify the
most general form of the first-order deformation in the interacting sector
at antighost number two
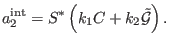 |
(120) |
The same conditions replaced in (97) enable us to write
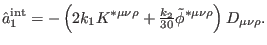 |
(121) |
Introducing (103) in (95) and then the resulting result
together with (101) in (93), we obtain
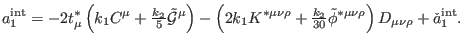 |
(122) |
Next, we determine
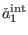 as the solution to the
homogeneous equation (68) for
as the solution to the
homogeneous equation (68) for  that is independently consistent
in antighost number zero, i.e. satisfies equation (96). According to
(75) for
that is independently consistent
in antighost number zero, i.e. satisfies equation (96). According to
(75) for  the general solution to equation (68) for
the general solution to equation (68) for  has the form
has the form
where all the quantities denoted by  ,
,  ,
,  ,
,  , or
, or  are bosonic, gauge-invariant tensors, and therefore they may depend only on
are bosonic, gauge-invariant tensors, and therefore they may depend only on
 given in (70) and their spacetime derivatives. The
functions
given in (70) and their spacetime derivatives. The
functions
 and
and
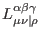 exhibit the mixed symmetry
exhibit the mixed symmetry  with respect to their lower indices
and, in addition,
with respect to their lower indices
and, in addition,
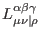 is completely
antisymmetric with respect to its upper indices. The remaining functions,
is completely
antisymmetric with respect to its upper indices. The remaining functions,  ,
,  ,
,  , and
, and  , are separately antisymmetric (where
appropriate) in their upper and respectively lower indices.
, are separately antisymmetric (where
appropriate) in their upper and respectively lower indices.
In order to determine all possible solutions (105) we demand that
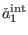 mixes the BF and
mixes the BF and  sectors and (for the
first time) explicitly implement the assumption on the derivative order of
the interacting Lagrangian discussed in the beginning of section 4
and structured in requirements i) and ii). Because all the terms involving
the functions
sectors and (for the
first time) explicitly implement the assumption on the derivative order of
the interacting Lagrangian discussed in the beginning of section 4
and structured in requirements i) and ii). Because all the terms involving
the functions  or
or  contain only BRST generators from the BF
sector, it follows that each such function must contain at least one tensor
contain only BRST generators from the BF
sector, it follows that each such function must contain at least one tensor
 defined in (72), with
defined in (72), with  as in (3). The corresponding terms from
as in (3). The corresponding terms from
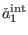 , if
consistent, would produce an interacting Lagrangian that does not agree with
requirement ii) with respect to the BF fields and therefore we must take
, if
consistent, would produce an interacting Lagrangian that does not agree with
requirement ii) with respect to the BF fields and therefore we must take
 |
(127) |
In the meantime, requirement ii) also restricts all the functions  and
and  to be derivative-free. Since the undifferentiated scalar field is
the only element among
to be derivative-free. Since the undifferentiated scalar field is
the only element among
 and their spacetime derivatives that
contains no derivatives, it follows that all
and their spacetime derivatives that
contains no derivatives, it follows that all  and
and  may depend at
most on
may depend at
most on  . Due to the fact that we work in
. Due to the fact that we work in  and taking into
account the various antisymmetry properties of these functions, it follows
that the only eligible representations are
and taking into
account the various antisymmetry properties of these functions, it follows
that the only eligible representations are
with 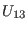 ,
,  , and
, and 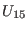 some real, smooth functions of
some real, smooth functions of  . The same observation stands for
. The same observation stands for
 and
and
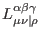 , so their tensorial behaviour can only
be realized via some constant Lorentz tensors. Nevertheless, there is no
such constant tensor in
, so their tensorial behaviour can only
be realized via some constant Lorentz tensors. Nevertheless, there is no
such constant tensor in  with the required mixed symmetry properties,
and hence we must put
with the required mixed symmetry properties,
and hence we must put
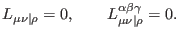 |
(130) |
Inserting results (106)-(109) in (105), it
follows that the most general (nontrivial) solution to equation (68)
for  that complies with all the working hypotheses, including that on
the differential order of the interacting Lagrangian, is given by
that complies with all the working hypotheses, including that on
the differential order of the interacting Lagrangian, is given by
 |
(131) |
By acting with 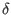 on (110) and using definitions (35
)-(52) we infer
on (110) and using definitions (35
)-(52) we infer
Comparing (111) with (96), we conclude that function 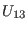 reduces to a real constant and meanwhile functions
reduces to a real constant and meanwhile functions  and
and 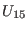 must vanish
must vanish
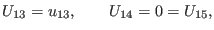 |
(136) |
so (110) becomes
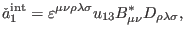 |
(137) |
wich produces trivial deformations because it is a trivial element from

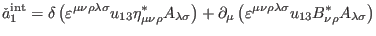 |
(138) |
and by further taking
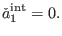 |
(139) |
As a consequence, we can safely take the nontrivial part of the first-order
deformation in the interaction sector in antighost number one, (104
), of the form
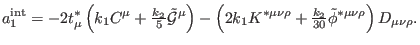 |
(140) |
In addition, (115) leads to
 |
(141) |
in (96). Replacing now (101) and (117) in (97), we are able to identify the piece of antighost number zero from
the first-order deformation in the interacting sector as
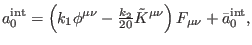 |
(142) |
where
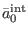 is the solution to the `homogeneous'
equation in antighost number zero
is the solution to the `homogeneous'
equation in antighost number zero
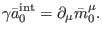 |
(143) |
We will prove in Appendix D that the only solution to (119)
that satisfies all our working hypotheses, including that on the derivative
order of the interacting Lagrangian, is
 , such
that the nontrivial part of the first-order deformation in the interaction
sector in antighost number zero reads as
, such
that the nontrivial part of the first-order deformation in the interaction
sector in antighost number zero reads as
 |
(144) |
The main conclusion of this section is that the general form of the
first-order deformation of the solution to the master equation as solution
to (58) for the model under study is expressed by
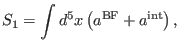 |
(145) |
where
 can be found in [32] and
can be found in [32] and
It is now clear that the first-order deformation is parameterized by seven
arbitrary, smooth functions of the undifferentiated scalar field (
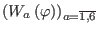 and
and
 corresponding to
corresponding to
 and by two arbitrary, real
constants (
and by two arbitrary, real
constants ( and
and  from
from
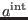 ). We will see in the
next section that the consistency of the deformed solution to the master
equation in order two in the coupling constant will restrict these functions
and constants to satisfy some specific equations.
). We will see in the
next section that the consistency of the deformed solution to the master
equation in order two in the coupling constant will restrict these functions
and constants to satisfy some specific equations.
Ashkbiz Danehkar
2018-03-26
![]() the nonintegrated density of the first-order deformation
(see (64)) becomes
the nonintegrated density of the first-order deformation
(see (64)) becomes
![]() and
and
![]() involve
different types of fields and that
involve
different types of fields and that
![]() separately satisfies an
equation of the type (62), it follows that
separately satisfies an
equation of the type (62), it follows that
![]() is
subject to the equation
is
subject to the equation
![]() can be chosen to stop
at antighost number
can be chosen to stop
at antighost number ![]()
![]() as solution to equation (68) for
as solution to equation (68) for ![]() has the general form expressed by (75) for
has the general form expressed by (75) for ![]() , with
, with
![]() from
from
![]() . Looking at formula (76)
and also at relation (81) in antighost number two and requiring
that
. Looking at formula (76)
and also at relation (81) in antighost number two and requiring
that
![]() mixes BRST generators from the BF and
mixes BRST generators from the BF and ![]() sectors, we get that the most general solution to (68) for
sectors, we get that the most general solution to (68) for ![]() reads as7
reads as7
![]() and using definitions (
35)-(52), we determine the solution
and using definitions (
35)-(52), we determine the solution
![]() under the form
under the form
![]() is the solution to the homogeneous
equation (68) in antighost number one, meaning that
is the solution to the homogeneous
equation (68) in antighost number one, meaning that
![]() is a nontrivial object from
is a nontrivial object from
![]() in pure
ghost number one and in antighost number one. It is useful to decompose
in pure
ghost number one and in antighost number one. It is useful to decompose
![]() like in (208)
like in (208)
![]() as the solution to the
homogeneous equation (68) for
as the solution to the
homogeneous equation (68) for ![]() that is independently consistent
in antighost number zero, i.e. satisfies equation (96). According to
(75) for
that is independently consistent
in antighost number zero, i.e. satisfies equation (96). According to
(75) for ![]() the general solution to equation (68) for
the general solution to equation (68) for ![]() has the form
has the form
![]() mixes the BF and
mixes the BF and ![]() sectors and (for the
first time) explicitly implement the assumption on the derivative order of
the interacting Lagrangian discussed in the beginning of section 4
and structured in requirements i) and ii). Because all the terms involving
the functions
sectors and (for the
first time) explicitly implement the assumption on the derivative order of
the interacting Lagrangian discussed in the beginning of section 4
and structured in requirements i) and ii). Because all the terms involving
the functions ![]() or
or ![]() contain only BRST generators from the BF
sector, it follows that each such function must contain at least one tensor
contain only BRST generators from the BF
sector, it follows that each such function must contain at least one tensor
![]() defined in (72), with
defined in (72), with ![]() as in (3). The corresponding terms from
as in (3). The corresponding terms from
![]() , if
consistent, would produce an interacting Lagrangian that does not agree with
requirement ii) with respect to the BF fields and therefore we must take
, if
consistent, would produce an interacting Lagrangian that does not agree with
requirement ii) with respect to the BF fields and therefore we must take
![]() on (110) and using definitions (35
)-(52) we infer
on (110) and using definitions (35
)-(52) we infer