A. No-go result for  in
in
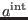
In agreement with (86), the general solution to the equation
 can be chosen to stop
at antighost number
can be chosen to stop
at antighost number 
 |
(220) |
where the components on the right-hand side of (181) are subject to
the equations (68) and (66)-(67) for  .
.
The piece
 as solution to equation (68) for
as solution to equation (68) for  has the general form expressed by (75) for
has the general form expressed by (75) for  , with
, with
 from
from
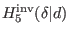 . According to (81)
at antighost number five, it follows that
. According to (81)
at antighost number five, it follows that
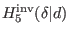 is spanned by the generic representatives (82). Since
is spanned by the generic representatives (82). Since
 should effectively mix the BF and the
should effectively mix the BF and the  tensor field
sectors in order to produce cross-couplings and (82) involves only
BF generators, it follows that one should retain from the basis elements
tensor field
sectors in order to produce cross-couplings and (82) involves only
BF generators, it follows that one should retain from the basis elements
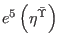 only the objects containing at
least one ghost from the
only the objects containing at
least one ghost from the  tensor field sector, namely
tensor field sector, namely
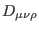 or
or  . Recalling that we work precisely in
. Recalling that we work precisely in  , we obtain
that the general solution to (68) for
, we obtain
that the general solution to (68) for  reduces to
reduces to
Each tilde object from the right-hand side of (182) means the Hodge
dual of the corresponding non-tilde element, defined in general by formula (
92). The elements  are dual to
are dual to
 as in (82), with
as in (82), with
 respectively replaced by the smooth function
respectively replaced by the smooth function
 depending only on the undifferentiated scalar field
depending only on the undifferentiated scalar field  .
.
Introducing (182) in equation (66) for  and recalling
definitions (35)-(52), we obtain
and recalling
definitions (35)-(52), we obtain
In (183)
 are dual to (83
), with
are dual to (83
), with
 . In
addition,
. In
addition,
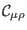 is implicitly defined by formula (74) so it is a ghost field of pure ghost number one without definite
symmetry/antisymmetry property,
is implicitly defined by formula (74) so it is a ghost field of pure ghost number one without definite
symmetry/antisymmetry property,
 is its
associated antifield, defined such that the antibracket
is its
associated antifield, defined such that the antibracket
 is equal to the `unit'
is equal to the `unit'

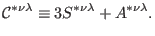 |
(227) |
The nonintegrated density
 stands for the
solution to the homogeneous equation (68) for
stands for the
solution to the homogeneous equation (68) for  , showing that
, showing that
 can be taken as a nontrivial element of
can be taken as a nontrivial element of
 in pure ghost number equal to four.
in pure ghost number equal to four.
At this stage it is useful to decompose
 as a
sum between two components
as a
sum between two components
 |
(228) |
where
 is the solution to (68) for
is the solution to (68) for  which is explicitly required by the consistency of
which is explicitly required by the consistency of
 in
antighost number three (ensures that (67) possesses solutions for
in
antighost number three (ensures that (67) possesses solutions for 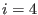 with respect to the terms from (183) containing the functions of the
type
with respect to the terms from (183) containing the functions of the
type  ) and
) and
 signifies the part of the
solution to (68) for
signifies the part of the
solution to (68) for  that is independently consistent in
antighost number three
that is independently consistent in
antighost number three
 |
(229) |
Using definitions (35)-(52) and decomposition (185
), by direct computation we obtain that
where we made the notations
 |
 |
![$\displaystyle -\check{c}_{3}+\tfrac{1}{12}\left( \tilde{U}_{1}\right) ^{\lambda...
... \vert\lambda
}^{\rho \alpha }\tilde{F}_{\alpha \nu \vert\sigma }\right] \notag$](img522.png) |
(232) |
| |
|
![$\displaystyle -\tfrac{1}{240}\left( \tilde{U}_{2}\right) ^{\lambda \sigma }\til...
... \vert\lambda }^{\rho \alpha }\tilde{F}_{\alpha \nu \vert\sigma }\right]
\notag$](img523.png) |
(233) |
| |
|
![$\displaystyle -\tfrac{1}{12}\left( \tilde{U}_{3}\right) ^{\lambda \sigma }\left...
...al{C}_{\lambda \rho }\mathcal{C}_{\sigma
\mu }\sigma ^{\rho \mu }\right] \notag$](img524.png) |
(234) |
| |
|
 |
(235) |
| |
|
 |
(236) |
| |
|
![$\displaystyle \left. +3F_{\qquad \vert\lambda }^{\mu \nu \rho }\tilde{D}_{\nu \...
...{C}_{\sigma \mu }-2\tilde{F}_{\rho \beta
\vert\sigma }S_{\mu }\right) \right] ,$](img527.png) |
(237) |
and
 are some local currents. In (187)-(189)
are some local currents. In (187)-(189)
 and
and
 denote the duals of (84) and (85) with
denote the duals of (84) and (85) with
 . In addition,
. In addition,
 represents the dual of
represents the dual of
 and
and
 the dual of
the dual of
 . Inspecting (187), it follows that the consistency of
. Inspecting (187), it follows that the consistency of
 in antighost number three, namely the existence of
in antighost number three, namely the existence of
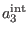 as solution to (67) for
as solution to (67) for 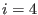 , requires the
conditions
, requires the
conditions
 |
(241) |
and
where we made the notations
 and
and
 . Nevertheless, from (189) it is obvious that
. Nevertheless, from (189) it is obvious that  is a nontrivial element from
is a nontrivial element from
 in pure
ghost number four, which does not reduce to a full divergence, and therefore
(190) requires that
in pure
ghost number four, which does not reduce to a full divergence, and therefore
(190) requires that
 , which further imply that all the
functions of the type
, which further imply that all the
functions of the type  must be some real constants
must be some real constants
 |
(244) |
Based on (192), it is clear that
 given by (
182) vanishes, and hence we can assume, without loss of nontrivial
terms, that
given by (
182) vanishes, and hence we can assume, without loss of nontrivial
terms, that
 |
(245) |
in (181).
Ashkbiz Danehkar
2018-03-26
![]() can be chosen to stop
at antighost number
can be chosen to stop
at antighost number ![]()
![]() as solution to equation (68) for
as solution to equation (68) for ![]() has the general form expressed by (75) for
has the general form expressed by (75) for ![]() , with
, with
![]() from
from
![]() . According to (81)
at antighost number five, it follows that
. According to (81)
at antighost number five, it follows that
![]() is spanned by the generic representatives (82). Since
is spanned by the generic representatives (82). Since
![]() should effectively mix the BF and the
should effectively mix the BF and the ![]() tensor field
sectors in order to produce cross-couplings and (82) involves only
BF generators, it follows that one should retain from the basis elements
tensor field
sectors in order to produce cross-couplings and (82) involves only
BF generators, it follows that one should retain from the basis elements
![]() only the objects containing at
least one ghost from the
only the objects containing at
least one ghost from the ![]() tensor field sector, namely
tensor field sector, namely
![]() or
or ![]() . Recalling that we work precisely in
. Recalling that we work precisely in ![]() , we obtain
that the general solution to (68) for
, we obtain
that the general solution to (68) for ![]() reduces to
reduces to
![]() and recalling
definitions (35)-(52), we obtain
and recalling
definitions (35)-(52), we obtain
![]() as a
sum between two components
as a
sum between two components
 represents the dual of
represents the dual of
 the dual of
the dual of
 . Nevertheless, from (189) it is obvious that
. Nevertheless, from (189) it is obvious that