B. No-go result for  in
in
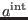
We have seen in Appendix A that we can always take (193) in (
181). Consequently, the first-order deformation of the solution to the
master equation in the interacting case stops at antighost number four
 |
(246) |
where the components on the right-hand side of (194) are subject to
the equations (68) and (66)-(67) for  .
.
The piece
 as solution to equation (68) for
as solution to equation (68) for  has the general form expressed by (75) for
has the general form expressed by (75) for  , with
, with
 from
from
 . According to (81)
at antighost number four, it follows that
. According to (81)
at antighost number four, it follows that
 is spanned by some representatives involving only BF generators. Since
is spanned by some representatives involving only BF generators. Since
 should again mix the BF and the
should again mix the BF and the  tensor field
sectors, it follows that one should retain from the basis elements
tensor field
sectors, it follows that one should retain from the basis elements
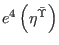 only the objects containing at
least one ghost from the
only the objects containing at
least one ghost from the  tensor field sector, namely
tensor field sector, namely
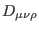 or
or  . The general solution to (68) for
. The general solution to (68) for  reads
as
reads
as
where each element generically denoted by
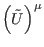 is the Hodge dual of an object similar to (83), but with
is the Hodge dual of an object similar to (83), but with  replaced by the arbitrary, smooth function
replaced by the arbitrary, smooth function  , depending on the
undifferentiated scalar field,
, depending on the
undifferentiated scalar field,
 reads as in (83) with
reads as in (83) with
 , and
, and  are two arbitrary, real
constants.
are two arbitrary, real
constants.
Introducing (195) in equation (66) for  and using
definitions (35)-(52), we determine the component of
antighost number three from
and using
definitions (35)-(52), we determine the component of
antighost number three from
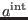 in the form
in the form
 |
 |
 |
(250) |
| |
|
![$\displaystyle +\tfrac{1}{2}\left( \tilde{U}_{5}\right) ^{\mu \nu }\left[ \left(...
...ho \lambda }\eta \tilde{D}_{\mu \rho }\mathcal{C}_{\nu \lambda }
\right] \notag$](img563.png) |
(251) |
| |
|
 |
(252) |
| |
|
![$\displaystyle -\tfrac{1}{2}\left( \tilde{U}_{9}\right) ^{\mu \nu }\sigma _{\alp...
...vert\nu }\tilde{D}^{\lambda \alpha }\tilde{D}
^{\rho \beta }\eta \right] \notag$](img565.png) |
(253) |
| |
|
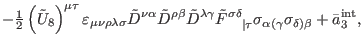 |
(254) |
where each
 is the Hodge dual of an
object of the type (84), with
is the Hodge dual of an
object of the type (84), with  replaced by the corresponding
function of the type
replaced by the corresponding
function of the type  . Here,
. Here,
 is the general
solution to the homogeneous equation (68) for
is the general
solution to the homogeneous equation (68) for  , showing that
, showing that
 is a nontrivial object from
is a nontrivial object from
 in pure ghost number three.
in pure ghost number three.
At this point we decompose
 in a manner similar
to (185)
in a manner similar
to (185)
 |
(255) |
where
 is the solution to (68) for
is the solution to (68) for  that ensures the consistency of
that ensures the consistency of
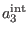 in antighost number
two, namely the existence of
in antighost number
two, namely the existence of
 as solution to (67
) for
as solution to (67
) for  with respect to the terms from
with respect to the terms from
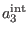 containing
the functions of the type
containing
the functions of the type  or the constants
or the constants  or
or  , while
, while
 is the solution to (68) for
is the solution to (68) for  which
is independently consistent in antighost number two
which
is independently consistent in antighost number two
 |
(256) |
Based on definitions (35)-(52) and taking into account
decomposition (197), we get by direct computation
where
 |
 |
 |
(261) |
| |
|
 |
(262) |
| |
|
 |
(263) |
| |
|
![$\displaystyle \left. +\tfrac{1}{2}\eta \left( \tilde{F}_{\mu \lambda \vert\nu }...
...\tilde{D}_{\mu }^{\quad \alpha }t_{\nu
\rho \vert\alpha }\right) \right] \notag$](img584.png) |
(264) |
| |
|
 |
(265) |
| |
|
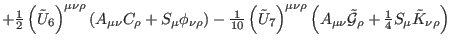 |
(266) |
| |
|
 |
(267) |
| |
|
 |
(268) |
| |
|
![$\displaystyle \left. +2F_{\mu \nu \rho \vert\sigma }\tilde{D}^{\nu \alpha }\lef...
...mbda }+\tilde{F}_{\quad \vert\lambda }^{\rho \beta }\eta
\right) \right] \notag$](img589.png) |
(269) |
| |
|
 |
(270) |
| |
|
 |
(271) |
 |
 |
 |
(272) |
| |
|
![$\displaystyle +\tfrac{q_{2}}{6}\sigma ^{\mu \nu }\tilde{D}_{\mu \alpha }\tilde{...
...{\ast \lambda \rho }\tilde{R}_{\beta \nu \vert\lambda \rho
}\eta \right] \notag$](img594.png) |
(273) |
| |
|
 |
(274) |
| |
|
 |
(275) |
| |
|
 |
(276) |
and
 are some local currents. Reprising an argument similar to
that employed in Appendix A between equations (190) and (193), we find that the existence of
are some local currents. Reprising an argument similar to
that employed in Appendix A between equations (190) and (193), we find that the existence of
 as solution to
equation (67) for
as solution to
equation (67) for  finally implies that
finally implies that 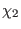 expressed by
(201) must vanish. This is further equivalent to the fact that all
the functions of the type
expressed by
(201) must vanish. This is further equivalent to the fact that all
the functions of the type  must be some real constants and both constants
must be some real constants and both constants
 must vanish
must vanish
Inserting (202) and (203) in (195), we conclude
that we can safely take
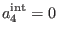 |
(279) |
in (194).
Ashkbiz Danehkar
2018-03-26
![]() as solution to equation (68) for
as solution to equation (68) for ![]() has the general form expressed by (75) for
has the general form expressed by (75) for ![]() , with
, with
![]() from
from
![]() . According to (81)
at antighost number four, it follows that
. According to (81)
at antighost number four, it follows that
![]() is spanned by some representatives involving only BF generators. Since
is spanned by some representatives involving only BF generators. Since
![]() should again mix the BF and the
should again mix the BF and the ![]() tensor field
sectors, it follows that one should retain from the basis elements
tensor field
sectors, it follows that one should retain from the basis elements
![]() only the objects containing at
least one ghost from the
only the objects containing at
least one ghost from the ![]() tensor field sector, namely
tensor field sector, namely
![]() or
or ![]() . The general solution to (68) for
. The general solution to (68) for ![]() reads
as
reads
as
![]() and using
definitions (35)-(52), we determine the component of
antighost number three from
and using
definitions (35)-(52), we determine the component of
antighost number three from
![]() in the form
in the form
![]() in a manner similar
to (185)
in a manner similar
to (185)