6 Computation of higher-order deformations
With the first-order deformation at hand, in the sequel we determine the
higher-order deformations of the solution to the master equation, governed
by equations (59)-(61), etc., which comply with our
working hypotheses.
In the first step we approach the second-order deformation,  , as
(nontrivial) solution to equation (59). If we denote by
, as
(nontrivial) solution to equation (59). If we denote by  the nonintegrated density of the antibracket
the nonintegrated density of the antibracket
 and by
and by  the nonintegrated density associated with
the nonintegrated density associated with  ,
,
 |
(149) |
then equation (59) takes the local form
 |
(150) |
with  a local current. By direct computation it follows that
a local current. By direct computation it follows that  decomposes as
decomposes as
 |
(151) |
where
 involves only BRST generators from the BF
sector and each term from
involves only BRST generators from the BF
sector and each term from
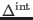 depends simultaneously on
the BRST generators of both sectors (BF and mixed symmetry
depends simultaneously on
the BRST generators of both sectors (BF and mixed symmetry  ), such
that
), such
that
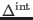 couples the two theories. Consequently,
decomposition (125) induces a similar one at the level of the
second-order deformation
couples the two theories. Consequently,
decomposition (125) induces a similar one at the level of the
second-order deformation
 |
(152) |
and equation (124) becomes equivalent to two equations, one for
the BF sector and the other for the interacting sector
Equation (127) has been completely solved in [32],
where it was shown that it possesses only the trivial solution
 |
(155) |
and, in addition, the seven functions
 and
and
 that parameterize
that parameterize
 are subject
to the following equations:
are subject
to the following equations:
Now, we investigate the latter equation, (128). By direct
computation
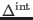 can be brought to the form
can be brought to the form
where
 is a local current and
is a local current and
 |
(164) |
In
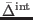 we used the notations
we used the notations
and the polynomials
 are listed in Appendix
E (see formulas (264)-(275)). It can be shown
that (137) cannot be written as a
are listed in Appendix
E (see formulas (264)-(275)). It can be shown
that (137) cannot be written as a  -exact modulo
-exact modulo  element
from local functions and therefore it must vanish
element
from local functions and therefore it must vanish
 |
(167) |
which further restricts the functions and constants that parameterize the
first-order deformation to obey the supplementary equations
As a consequence, the consistency of the first-order deformation at order
two in the coupling constant (the existence of local solutions to equation (
59)) on the one hand restricts the functions and constants that
parameterize  to fulfill equations (130)-(135) and (
141)-(142) and, on the other hand, enables us (via formulas (
123), (126), (128), (129), (136
), and (140)) to infer the second-order deformation as
to fulfill equations (130)-(135) and (
141)-(142) and, on the other hand, enables us (via formulas (
123), (126), (128), (129), (136
), and (140)) to infer the second-order deformation as
![$\displaystyle S_{2}=S_{2}^{\mathrm{int}}=\int d^{5}x\left[ \tfrac{3}{2}\left( k...
...t( k_{1}\phi ^{\mu \nu }-\tfrac{k_{2}}{20}\tilde{K}^{\mu \nu }\right) \right] .$](img407.png) |
(170) |
In the second step we solve the equation that governs the third-order
deformation, namely, (60). If we make the notations
 |
(171) |
then equation (60) takes the local form
 |
(172) |
with  a local current. By direct computation we obtain
a local current. By direct computation we obtain
 |
(173) |
where
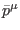 is a local current and the functions
is a local current and the functions
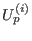 appearing in the right-hand side of (146) are listed in
Appendix E (see formulas (276)-(284)). Taking into
account the result that the functions and constants that parameterize both
the first- and second-order deformations satisfy equations (130)-(
135) and (141)-(142) and comparing (146) with
equation (145), it results that the third-order deformation can
be chosen to be completely trivial
appearing in the right-hand side of (146) are listed in
Appendix E (see formulas (276)-(284)). Taking into
account the result that the functions and constants that parameterize both
the first- and second-order deformations satisfy equations (130)-(
135) and (141)-(142) and comparing (146) with
equation (145), it results that the third-order deformation can
be chosen to be completely trivial
 |
(174) |
Related to the equation that governs the fourth-order deformation, namely, (
61), we have that
 |
(175) |
From (148) and (61) we find that  is completely
trivial
is completely
trivial
 |
(176) |
Along a similar line, it can be shown that all the remaining higher-order
deformations  (
( ) can be taken to vanish
) can be taken to vanish
 |
(177) |
The main conclusion of this section is that the deformed solution to the
master equation for the model under study, which is consistent to all orders
in the coupling constant, can be taken as
 |
(178) |
where  reads as in (53),
reads as in (53),  is given in (121) with
is given in (121) with
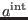 of the form (122), and
of the form (122), and  is expressed by (143). It represents the most general solution
that complies with all our working hypotheses (see the discussion from the
beginning of section 4). We cannot stress enough that the (seven)
functions and (two) constants that parameterize the fully deformed solution
to the master equation are no longer independent. They must obey equations (
130)-(135) and (141)-(142).
is expressed by (143). It represents the most general solution
that complies with all our working hypotheses (see the discussion from the
beginning of section 4). We cannot stress enough that the (seven)
functions and (two) constants that parameterize the fully deformed solution
to the master equation are no longer independent. They must obey equations (
130)-(135) and (141)-(142).
Ashkbiz Danehkar
2018-03-26
![]() , as
(nontrivial) solution to equation (59). If we denote by
, as
(nontrivial) solution to equation (59). If we denote by ![]() the nonintegrated density of the antibracket
the nonintegrated density of the antibracket
![]() and by
and by ![]() the nonintegrated density associated with
the nonintegrated density associated with ![]() ,
,
![]() to fulfill equations (130)-(135) and (
141)-(142) and, on the other hand, enables us (via formulas (
123), (126), (128), (129), (136
), and (140)) to infer the second-order deformation as
to fulfill equations (130)-(135) and (
141)-(142) and, on the other hand, enables us (via formulas (
123), (126), (128), (129), (136
), and (140)) to infer the second-order deformation as