D. No-go result for  in
in
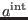
The solution to the `homogeneous' equation (119) can be represented as
 |
(307) |
where
and
 is a nonvanishing, local current.
is a nonvanishing, local current.
According to the general result expressed by (75) in both antighost
and pure ghost numbers equal to zero, equation (217) implies
![$\displaystyle \bar{a}_{0}^{\prime \mathrm{int}}=\bar{a}_{0}^{\prime \mathrm{int}}\left( \left[ F_{\bar{A}}\right] \right) ,$](img649.png) |
(310) |
where
 are listed in (75). Solution (219) is
assumed to provide a cross-coupling Lagrangian. Therefore, since
are listed in (75). Solution (219) is
assumed to provide a cross-coupling Lagrangian. Therefore, since
 is the most general gauge-invariant quantity depending
on the field
is the most general gauge-invariant quantity depending
on the field
 , it follows that each interaction vertex
from
, it follows that each interaction vertex
from
 is required to be at least linear
in
is required to be at least linear
in
 and to depend at least on a BF field.
But
and to depend at least on a BF field.
But
 contains two spacetime derivatives, so
the emerging interacting field equations would exhibit at least two
spacetime derivatives acting on the BF field(s) from the interaction
vertices. Nevertheless, this contradicts the general assumption on the
preservation of the differential order of each field equation with respect
to the free theory (see assumption ii) from the beginning of section 4), so we must set
contains two spacetime derivatives, so
the emerging interacting field equations would exhibit at least two
spacetime derivatives acting on the BF field(s) from the interaction
vertices. Nevertheless, this contradicts the general assumption on the
preservation of the differential order of each field equation with respect
to the free theory (see assumption ii) from the beginning of section 4), so we must set
 |
(311) |
Next, we solve equation (218). In view of this, we decompose
 with respect to the number of derivatives
acting on the fields as
with respect to the number of derivatives
acting on the fields as
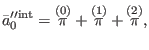 |
(312) |
where each
 contains precisely
contains precisely  spacetime
derivatives. Of course, each
spacetime
derivatives. Of course, each
 is required to mix the BF
and
is required to mix the BF
and  field sectors in order to produce cross-interactions. In
agreement with (221), equation (218) is equivalent to
field sectors in order to produce cross-interactions. In
agreement with (221), equation (218) is equivalent to
Using definitions (45)-(47) and an integration by parts it is
possible to show that
From (225) we observe that
 is solution to (222) if and only if the following conditions are satisfied
simultaneously
is solution to (222) if and only if the following conditions are satisfied
simultaneously
Because
 is derivative-free, the solutions to equations
(226)-(227) read as
is derivative-free, the solutions to equations
(226)-(227) read as
where
 ,
,  ,
,  ,
,
 ,
,
 , and
, and
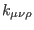 are some real, constant tensors. In
addition,
are some real, constant tensors. In
addition,
 display the same mixed symmetry
properties like the tensor field
display the same mixed symmetry
properties like the tensor field
 and
and
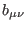 ,
,
 , and
, and
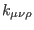 are completely antisymmetric. Because
there are no such constant tensors in
are completely antisymmetric. Because
there are no such constant tensors in  , we conclude that (226
)-(227) possess only the trivial solution, which further implies
that
, we conclude that (226
)-(227) possess only the trivial solution, which further implies
that
 |
(323) |
Related to equation (223), we use again definitions (45)-(
47) and integrate twice by parts, obtaining
Inspecting (231), we observe that
 satisfies
equation (223) if and only if the following relations take place
simultaneously
satisfies
equation (223) if and only if the following relations take place
simultaneously
The solutions to equations (232)-(233) are expressed by
where the quantities
 ,
,
 ,
, 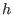 ,
,
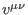 ,
, 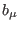 ,
,
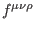 , and
, and
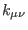 are some tensors depending at most on the undifferentiated fields
are some tensors depending at most on the undifferentiated fields
 from (2). In addition, they display the
symmetry/antisymmetry properties
from (2). In addition, they display the
symmetry/antisymmetry properties
and
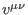 ,
,
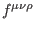 , and
, and
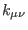 are completely
antisymmetric. Because both tensors
are completely
antisymmetric. Because both tensors
 and
and
 are derivative-free, their are related through
are derivative-free, their are related through
 |
(335) |
Using successively properties (237)-(239) and formula (240), it can be shown that
 is
completely antisymmetric. This last property together with (239)
leads to
is
completely antisymmetric. This last property together with (239)
leads to
which replaced in the latter equality from (234) produces
This means that the entire dependence of
 on
on
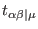 is trivial (reduces to a full divergence), and therefore
is trivial (reduces to a full divergence), and therefore
 can at most describe self-interactions in the BF
sector. Since there is no nontrivial solution to (223) that mixes
the BF and
can at most describe self-interactions in the BF
sector. Since there is no nontrivial solution to (223) that mixes
the BF and  field sectors, we can safely take
field sectors, we can safely take
 |
(336) |
In the end of this section we analyze equation (224). Taking one
more time into account definitions (45)-(47), it is easy to
see that (224) implies that the EL derivatives of
 are subject to the equations
are subject to the equations
Because
 (and also its EL derivatives) contains two
spacetime derivatives, the solution to both equations from (242) is
of the type
(and also its EL derivatives) contains two
spacetime derivatives, the solution to both equations from (242) is
of the type
 |
(340) |
where
 depends only on the
undifferentiated fields
depends only on the
undifferentiated fields
 and exhibits the mixed
symmetry
and exhibits the mixed
symmetry
 . This means that
. This means that
 is simultaneously antisymmetric in its first three and
respectively last two indices and satisfies the identity
is simultaneously antisymmetric in its first three and
respectively last two indices and satisfies the identity
![$ \bar{\tau}^{[\mu
\nu \rho \vert\alpha ]\beta }=0$](img719.png) . The solutions to the remaining equations, (243) and (247), can be represented as
. The solutions to the remaining equations, (243) and (247), can be represented as
where the functions
 ,
,
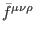 , and
, and
 are completely antisymmetric and contain a single
spacetime derivative.
are completely antisymmetric and contain a single
spacetime derivative.
Let  be a derivation in the algebra of the fields
be a derivation in the algebra of the fields
 ,
,
 ,
,  ,
,
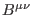 ,
,
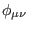 ,
,
 , and of their derivatives, which counts the powers of these fields and of
their derivatives
, and of their derivatives, which counts the powers of these fields and of
their derivatives
We emphasize that  does not `see' either the scalar field
does not `see' either the scalar field  or
its spacetime derivatives. It is easy to check that for every nonintegrated
density
or
its spacetime derivatives. It is easy to check that for every nonintegrated
density  we have
we have
If
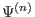 is a homogeneous polynomial of degree
is a homogeneous polynomial of degree  in the fields
in the fields
 ,
,  ,
,  ,
,
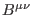 ,
,
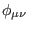 ,
,
 and their derivatives (such a polynomial may
depend also on
and their derivatives (such a polynomial may
depend also on  and its spacetime derivatives, but the homogeneity
does not take them into consideration since
and its spacetime derivatives, but the homogeneity
does not take them into consideration since  is allowed to be a
series in
is allowed to be a
series in  ), then
), then
Based on results (245)-(247), we can write
We decompose
 along the degree
along the degree  as
as
 |
(350) |
where
 (
( in (
251) because
in (
251) because
 , and hence every
, and hence every
 , is assumed to describe cross-interactions between the BF model
and the tensor field with the mixed symmetry
, is assumed to describe cross-interactions between the BF model
and the tensor field with the mixed symmetry  ), and find that
), and find that
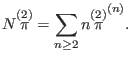 |
(351) |
Comparing (252) with (250), it follows that decomposition (
251) induces a similar one with respect to each function
 ,
,  ,
,
 ,
,
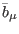 ,
,
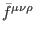 , and
, and

Inserting (253) and (254) in (250) and comparing
the resulting expression with (252), we get
Replacing the last result, (255), into (251), we further
obtain
where
So far, we showed that the solution to (224) can be put in the form (
256). By means of definitions (36)-(37), we can
bring (256) to the expression
The 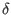 -exact modulo
-exact modulo  terms in the right-hand side of (259)
produce purely trivial interactions, which can be eliminated via field
redefinitions. This is due to the isomorphism
terms in the right-hand side of (259)
produce purely trivial interactions, which can be eliminated via field
redefinitions. This is due to the isomorphism
 in all positive
values of the ghost number and respectively of the pure ghost number [42], which at
in all positive
values of the ghost number and respectively of the pure ghost number [42], which at  allows one to state that any solution of equation (
224) that is
allows one to state that any solution of equation (
224) that is 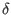 -exact modulo
-exact modulo  is in fact a trivial cocycle
from
is in fact a trivial cocycle
from
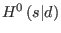 . In conclusion, the only nontrivial solution
to (224) can be written as
. In conclusion, the only nontrivial solution
to (224) can be written as
 |
(362) |
where
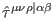 displays the mixed symmetry
displays the mixed symmetry
 , is derivative-free, and is required to depend at least
on one field from the BF sector. But
, is derivative-free, and is required to depend at least
on one field from the BF sector. But
 already contains two spacetime derivatives, so such a
already contains two spacetime derivatives, so such a
 disagrees with the hypothesis on the differential order of the interacting
field equations (see also the discussion following formula (219)),
which means that we must set
disagrees with the hypothesis on the differential order of the interacting
field equations (see also the discussion following formula (219)),
which means that we must set
 |
(363) |
Substituting results (230), (241), and (261) into
decomposition (221), we obtain
 |
(364) |
which combined with (220) proves that indeed there is no nontrivial
solution to the `homogeneous' equation (119) that complies with all
the working hypotheses
 |
(365) |
Ashkbiz Danehkar
2018-03-26
![]() with respect to the number of derivatives
acting on the fields as
with respect to the number of derivatives
acting on the fields as

![]() are subject to the equations
are subject to the equations
![]() be a derivation in the algebra of the fields
be a derivation in the algebra of the fields
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() , and of their derivatives, which counts the powers of these fields and of
their derivatives
, and of their derivatives, which counts the powers of these fields and of
their derivatives